El Barcelona denuncia a Mourinho por ensuciar su prestigio y su historia
"Los líderes, como son los entrenadores, deberían hablar solo de fútbol y no de cuestiones que incitan a la violencia", ha afirmado el portavoz del club, Toni Freixa
"Los líderes, como son los entrenadores, deberían hablar solo de fútbol y no de cuestiones que incitan a la violencia", ha afirmado el portavoz del club, Toni Freixa

Futbolista argentino

El anuncio de los empresarios vascos y navarros de que ETA ha cesado de extorsionarles es un avance en el camino hacia el final de la banda impulsado por la izquierda 'abertzale'
Radiografía del paro
La entidad cordobesa, intervenida por el Banco de España el pasado mayo, es la única caja en números rojos
El Premio Internacional de Alcobendas reconoce la trayectoria de García Rodero
El 'número dos' de Aguirre acusa al Ejecutivo de "discriminar" a las autonomías que hacen los deberes
Los 7.000 trabajadores del servicio de limpieza viaria de la capital pararán desde el 12 de mayo
El candidato socialista critica "su falta de deslealtad institucional" y la acusa de llevar a cabo una estrategia de confrontación territorial

José Garay, profesor de la <a href="http://www.unizar.es/" target="blank">Universidad de Zaragoza</a>, presenta el séptimo desafío de EL PAÍS con el que celebramos el <a href="http://www.rsme.es/centenario/" target="blank">centenario de la Real Sociedad Matemática Española</a>. Las respuestas pueden enviarse a <a href="mailto:problemamatematicas@gmail.com">problemamatematicas@gmail.com</a> antes de la medianoche del lunes 2 de mayo (00.00 horas del martes). Entre los acertantes sortearemos una <a href="http://www.elpais.com/promociones/matematicas/">biblioteca matemática</a> como la que ofrece cada semana EL PAÍS. Este domingo, por 9,95 euros con el periódico en el quiosco, <i>La cuarta dimensión</i>, de Raúl Ibáñez.<p><b>Nota importante</b>: Para evitar dudas y en atención a nuestros lectores sordos, incluimos a continuación el enunciado del problema por escrito.</p><p> <b>Enunciado:</b> Sabemos que al pulsar las teclas blancas de un piano se reproducen periódicamente las siete notas de la escala musical Do, Re, Mi, Fa, Sol, La y Si. Por lo tanto aunque el piano tenga muchas teclas, solamente podemos escuchar las siete notas de la escala, eso sí, en diversas octavas. Los pianos reales tienen un número limitado de teclas, pero para nuestro problema vamos a imaginar un piano con un teclado tan largo como nos sea necesario. E imaginaremos que pulsamos SÓLO las teclas blancas.</p><p> Primero pulsamos el primer Do que tenemos por la izquierda. A continuación pulsamos la siguiente tecla, que naturalmente será un Re. Luego saltamos una tecla y tocamos el Fa. Ahora saltamos dos teclas y tocamos el Si. Seguidamente saltamos tres teclas y tocamos el Fa, ya en la segunda octava. Y continuamos el proceso saltando cada vez una tecla más que la vez anterior. Como hemos supuesto que nuestro piano tiene tantas teclas como queramos supongamos que hemos llegado a tocar 7.000 teclas. Y hacemos dos preguntas:</p><p> 1. ¿Cuántas teclas habremos tocado que corresponden a la nota Do?</p><p> 2. ¿Habrá alguna nota que no haya sido pulsada en ningún momento?</p><p> <b>Aclaración:</b> Por si acaso alguien se confunde y piensa que nuestro piano tiene solo 7.000 teclas, hemos de insistir en que 7.000 es el número de teclas que tocamos, y dado que entre dos teclas pulsadas hay muchas que no se tocan, se deduce que nuestro imaginario piano tiene muchas más que esas 7.000. Y aunque este número no es necesario para resolver el problema podemos afirmar que el piano debe tener unos 24 millones y medio de teclas blancas. </p> <a href="http://www.elpais.com/articulo/sociedad/salvar/seguro/29/presos/elpepusoc/20110426elpepusoc_4/Tes"><b>CONSULTA LOS PROBLEMAS ANTERIORES</b></a>
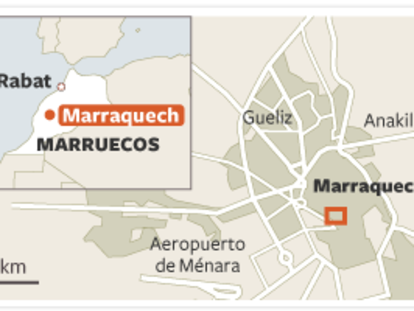
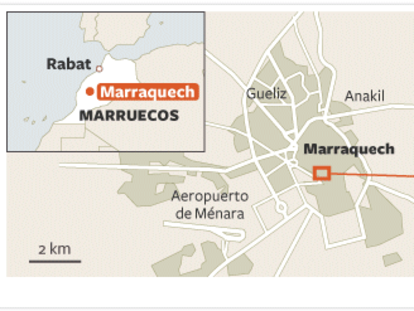
El atentado de hoy es uno de los más graves en cuanto al número de víctimas mortales de los últimos 17 años
Durante las cuatro horas de interrogatorio el comisario Carlos Germán afirma que el movil de la delación fue "político"
Atentado en Marraquech

La locomotora europea logra reducir de nuevo el número de desempleados en abril hasta su nivel más bajo desde la reunificación con 2,97 millones
Se desconoce la cantidad y la organización a la que los príncipes de Asturias y la reina doña Sofía entregarán el dinero
Palestinian former inmate now living in Spain had no proven links to Al Qaeda
El impuesto revolucionario recaudó 115 millones de euros entre 1978 y 2008, según un informe
La primera potencia mundial reduce su ritmo crecimiento en el primer trimestre al 1,8% del 3,1% de finales de 2010
El departamento que dirige Elena Salgado rebaja al 67,2% el endeudamiento público para este año
Exigen la nulidad del juicio "político" en el que fueron condenados
Editores, distribuidores y libreros organizan un acto en Madrid para solicitar a las instituciones españolas y europeas la cancelación del impuesto
ZTE Light Pro funciona con Android y lo tiene en exclusiva la operadora española
La consejera lamenta que los sindicatos "no hayan sido capaces de tener presente la realidad actual"