Jugando a ser Victor D’Hondt

Angélica Benito Sualdea y Adolfo Quirós Gracián, profesores de Matemáticas en la Universidad Autónoma de Madrid nos presentan el segundo de los tres desafíos que EL PAÍS y la Real Sociedad Matemática Española van a proponer en este periodo de intensa actividad electoral.

En esta ocasión trata de cómo afectan las circunscripciones a la aplicación del método D'Hondt (llamado también método de los divisores naturales o, en Estados Unidos, método de Jefferson), que es el que rige en España la mayoría de los procesos electorales. Los lectores pueden enviar sus respuestas hasta las 00.00 del jueves 25 de abril (la medianoche del miércoles al jueves, hora peninsular española) a problemamatematicas@gmail.com.

A continuación, para aclarar dudas, añadimos el enunciado del problema por escrito. Recordemos que el método D'Hondt procede como sigue para repartir E escaños. Se dividen los votos de cada partido sucesivamente entre 1, 2, 3,… hasta E, y se asignan los escaños a los partidos a los que correspondan los E mayores cocientes. Para dar un ejemplo, supongamos que tres partidos, A, B y C, que han obtenido respectivamente 240, 150 y 90 votos, deben repartirse 4 escaños. Haríamos una tabla como esta (aunque en realidad no es necesario calcularla entera):

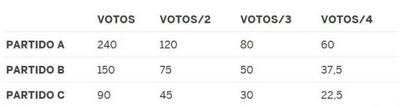
Si vamos mirando los cocientes mayores, el primer escaño se lo llevaría A (por el 240), el segundo B (150), el tercero de nuevo A (120) y el cuarto C (90). La gran mayoría de la falta de proporcionalidad en el Congreso de los Diputados no viene del uso del método D'Hondt, sino de que la elección se realiza en 52 circunscripciones, y por tanto son en realidad 52 elecciones distintas, en la mayoría de las cuales se reparten pocos diputados. Por ejemplo, en las elecciones del próximo 28 de abril, a 21 de las 52 circunscripciones les corresponden cuatro o menos escaños, siendo imposible que en ninguna de ellas obtengan representación cinco partidos.

La existencia de 52 circunscripciones dificulta también hacer predicciones sobre los escaños a partir de encuestas con una muestra de tamaño suficiente para toda España, pero quizás no para cada provincia individualmente. A esta dificultad se dirige nuestro desafío. Supongamos que queremos repartir, usando el método D'Hondt, seis escaños entre tres partidos, A, B y C, que han obtenido respectivamente 63, 68 y 69 votos (si parecen números pequeños, pueden ser "miles de votos" sin que el resultado varíe). La primera parte de la tabla quedaría así:

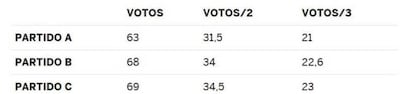
Como 69/3=23<31,5=63/2, el reparto de los 6 escaños daría 2 a cada partido. Imaginemos ahora que estos 200 electores en realidad viven en 2 provincias, 100 en cada una, y que en cada provincia se eligen 3 diputados, pero no sabemos cómo se distribuyen los votos entre las provincias. El desafío consiste en dar el número máximo y mínimo de escaños que puede lograr el partido A según estén distribuidos los 200 electores. De manera similar al desafío anterior, hay que dar un ejemplo en el que obtenga el máximo, otro en el que obtenga el mínimo, y explicar rigurosamente por qué A no puede lograr ni más ni menos escaños.

Esperamos vuestras respuestas.