Así amañaba los distritos el malévolo gobernador
Solución al primer desafío matemático electoral que plantean EL PAÍS y la RSME

Ya hay solución para el primero de los desafíos matemáticos electorales presentado por EL PAÍS y la Real Sociedad Matemática Española. Angélica Benito Sualdea y Adolfo Quirós Gracián, profesores de la Universidad Autónoma de Madrid, propusieron el desafío y nos dan ahora la solución.
Recordemos que teníamos 225 electores, grises y ocres, que deben elegir 15 representantes que represente cada uno a 15 votantes, y se trataba de ver qué diseño de distritos era más beneficioso para el partido gris con dos distribuciones geográficas distintas de los votantes. El único requisito era que los distritos no tuviesen dos trozos.
Como en cada distrito hay 15 votantes, son necesarios ocho para ganarlo. En las dos situaciones que proponíamos, los grises cuentan con 105 votantes y 105/8=13,125. Por tanto, el máximo de representantes que pueden conseguir en cualquier caso son 13.
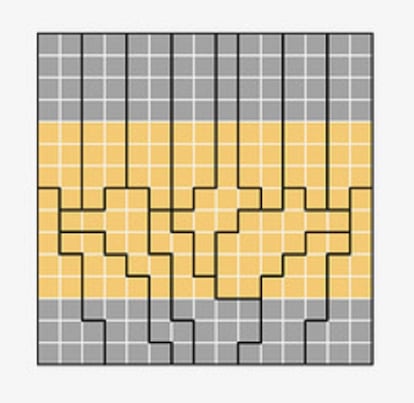
Pero con la primera distribución de votantes, que era la de esta imagen,

cualquier distrito que una a los votantes grises de arriba con los de abajo tiene que pasar por ocho votantes amarillos y, por tanto, el partido amarillo ganaría ese distrito.
Mirando sólo los 60 votantes grises de arriba, tenemos 60/8=7,5 y, por tanto, se pueden obtener siete representantes en la franja de arriba. Con los 45 votos de abajo se tiene 45/8=5,625 y los grises no pueden superar ahí los cinco representantes. Así pues, con esa distribución, lo más que pueden obtener los grises son 12 representantes, y los consiguen, por ejemplo, así:
La segunda distribución de los votantes era esta:

Ahora los grises sí que pueden alcanzar los 13 representantes. Por ejemplo, diseñando así los distritos:

Se han recibido dentro del plazo establecido 130 soluciones, procedentes tanto de España como de otros países europeos y americanos. El 93% de ellas son correctas y casi todas están justificadas adecuadamente, con algunos ejemplos de distritos especialmente bien dibujados, sea por su simetría, disposición o colorido. Es el caso de lo que nos envían Ruth L., Rafael C. o Ángel P.
También hay soluciones "familiares", como la que han encontrado conjuntamente Xavier V. y su hijo, o las que han elaborado, en este caso por separado, Claudia y César C.
Algunos lectores, entre ellos Eva G. o Asier G., manifiestan su desazón por lo que se concluye del desafío. Podría tranquilizarles el comentario de Javier R., quien señala que "en la práctica un gobernador nunca podrá conocer con certeza la decisión que finalmente adopten los votantes".
La RSME ha decidido seleccionar un lector entre los que han resuelto el desafío para enviarle un ejemplar del libro Desafíos matemáticos, que recoge en versiones ampliadas los que se publicaron originalmente en EL PAÍS con ocasión del centenario de la sociedad y que forma parte de la Biblioteca Estímulos Matemáticos que publica conjuntamente con Editorial SM. El agraciado ha sido Rodrigo V.
Hayáis dado o no con la respuesta, esperamos que el desafío os haya resultado interesante. Nos sentiremos satisfechos si se ha cumplido lo que amablemente nos dice Luis M. del P.: "Es una excelente forma de hablar sobre las elecciones sin polemizar (demasiado) y divirtiéndose".
Si ha sido así, os esperamos en el siguiente, que volverá a tratar sobre circunscripciones, pero esta vez en relación con el método D'Hondt.
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.




























































