Árboles

En el Hex, el empate es imposible. No pueden completar cadena ambos jugadores (aunque el segundo jugador pueda seguir jugando si la completa el primero) porque una cadena que une lados opuestos del tablero lo divide en dos partes totalmente separadas e impide, por tanto, que se conecten entre sí los tramos de fichas rivales que intentan unir los otros dos lados. Pero otra posibilidad de empate sería que ninguno de los dos jugadores pudiera completar su cadena; sin embargo, esto tampoco es posible: si ambos jugadores van colocando fichas hasta llenar el tablero, se completará necesariamente una cadena, aun en el supuesto de que deliberadamente intenten evitarlo (en el comentario 47 de hace un par de semanas se puede ver una demostración detallada).

La ventaja de la superelipse sobre la elipse, para trazar una rotonda en una plaza rectangular, es que llena mejor el espacio -se ciñe más a los lados del rectángulo- y facilita la circulación de los vehículos (un circuito elíptico tiene la desventaja de que parece circular pero no lo es, lo que podría despistar a los conductores).

A medida que aumenta el exponente de la ecuación de la superelipse, se aproxima más al rectángulo circunscrito, y en el límite, cuando n tiende a infinito, coincide con él.

La curiosa propiedad del “superhuevo” de Piet Hein es que, al contrario que los elipsoides de revolución o los huevos, permanece en equilibrio sobre cualquiera de sus extremos, lo cual lo popularizó, en pequeño formato, como objeto de regalo.

Grafos arbóreos

En las últimas semanas hemos resuelto algunos problemas utilizando grafos, y más concretamente “árboles”, aunque sin nombrarlos. Un grafo es un conjunto de puntos, llamados vértices o nodos, unidos por una serie de líneas, llamadas lados o aristas, que representan relaciones binarias entre los elementos de un conjunto. Si desde cualquiera de los puntos del grafo se puede ir a cualquier otro recorriendo aristas, es un grafo conexo. Y si en un grafo conexo no hay circuitos cerrados, se denomina “árbol”, por su semejanza con los árboles de la naturaleza. El Árbol de la Ciencia de Ramón Llull y el Árbol de Porfirio son ilustres precursores de los grafos arbóreos.

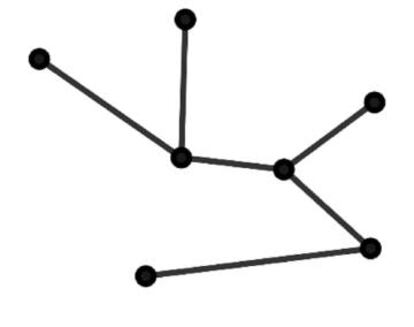
Es evidente que con dos puntos podemos formar un único árbol, y lo mismo con tres. Con cuatro puntos podemos formar dos árboles distintos: los cuatro puntos alineados o formando una Y. En la figura vemos un árbol de siete nodos; ¿cuántos distintos podemos formar? ¿Tendrán todos el mismo número de aristas? (Una pequeña advertencia: es fácil confundirse y pensar que son distintos dos árboles que en realidad son equivalentes).

¿Qué podemos decir de la secuencia numérica que expresa el número de árboles distintos que se pueden formar con 2, 3, 4, 5… nodos? ¿Qué ejemplos de árboles (además de los propios árboles) hay en la naturaleza? ¿Y en las obras humanas?

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos Maldita física, Malditas matemáticas o El gran juego. Fue guionista de La bola de cristal.