¿Hablan las células el lenguaje de las matemáticas?

Tanto durante el desarrollo embrionario como en el individuo adulto, las células necesitan saber dónde están, cuántas son, con qué otras tienen que interactuar y cuánto tienen que proliferar para formar tejidos diferentes de tamaño y forma concretos. Esto requiere que conversen entre ellas, a través de la comunicación celular, que no es más que la capacidad que tienen todas las células de intercambiar información fisicoquímica con el medio ambiente y con otras células para poder actuar coordinadamente. Sin embargo, aún existen muchos interrogantes sobre este proceso: ¿cómo es la comunicación entre células adyacentes o alejadas? ¿Cómo se emiten, reciben e interpretan las señales moleculares en esta comunicación? ¿Están estas señales orientadas y dirigidas hacia células más predispuestas a su recepción? Y la pregunta más importante, ¿cómo podemos influir en este proceso de comunicación? Las matemáticas son una herramienta esencial para responder a estas cuestiones de interés biológico.

En 1952 el matemático inglés Alan Turing sentó las bases de la modelización matemática de la morfogénesis. Durante este proceso la comunicación celular es fundamental, ya que es a través de señales cómo se controlan los códigos genéticos que hacen que la célula modifique su comportamiento, o incluso su misma esencia, para construir o diseñar un patrón determinado (forma, tamaño, diferenciación tisular, etc.). Turing atribuyó la formación de patrones a mecanismos de difusión de estas señales (en concreto, al movimiento aleatorio de las señales, que aparece como resultado de interacciones con las moléculas del fluido extracelular) junto a procesos de reacción química entre ellas (activación o represión de la señal) en el entorno que rodea a las células.

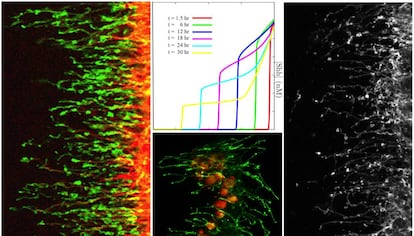
En esta última década, el enorme avance de las técnicas de microscopía y el desarrollo de herramientas moleculares permitieron seguir con más detalle la dinámica de estas señales, y gracias a ello se pudo observar una realidad bien diferente a la intuida por Turing. El conocimiento actual nos lleva a considerar que las células se comunican por contacto directo incluso cuando se encuentran muy alejadas entre sí. El proceso de transferencia de señales se lleva a cabo mediante extensiones retráctiles de la membrana celular (denominadas filopodios o nanotubos). La información bioquímica a transmitir circula por estas estructuras, como ocurre durante la comunicación neuronal, en lo que parece ser un sistema genérico de comunicación.

La célula receptora interpreta estas señales mediante las denominadas rutas de señalización, a las que se asocian determinadas moléculas que actúan desde el inicio del estímulo para que las células respondan. Estas rutas son específicas para cada señal y cada una regula la expresión de unos genes concretos. Entre ellas, la ruta de Hedgehog-Gli, en la que centramos nuestra investigación, es fundamental durante el desarrollo animal y en el crecimiento tumoral. En este proceso están involucrados aspectos puramente mecánicos (la dinámica de elongación y retracción de filopodios, los factores responsables del direccionamiento de la información, etc.) y aspectos moleculares, cuyo resultado perfectamente coordinado no da opción a la aleatoriedad.

Todo este perfecto engranaje puede ser modelado por ecuaciones diferenciales en las diversas escalas del proceso (los tiempos de transmisión de la señal y de reacción de la célula son diferentes, al igual que el recorrido espacial de la señal fuera y dentro de la célula), que permiten predecir y aprender de su dinámica. Los modelos matemáticos en biología ayudan a revelar nuevos fenómenos, dinámicas no esperadas o patrones evolutivos, para formular y corroborar nuevos experimentos, y a direccionarlos en la búsqueda de respuestas.

Prototipos

En este caso, el conocimiento básico de lo micro o lo nano nos posibilita establecer prototipos y trasladarlos a una escala macroscópica, la del tejido o tumor. Con estos métodos podemos saber cómo se orientan los filopodios que median la señalización celular, cómo de específico es el proceso en cada tipo de señal y la posibilidad de que comportamientos celulares o moleculares individuales deriven en un comportamiento colectivo. Con intereses terapéuticos, esta modelización es clave para sentar los principios para la identificación de nuevos inhibidores o promotores de estas rutas de señalización que cuando están alteradas son causantes de patologías.

De esta manera, desarrollos matemáticos, como la teoría del potencial o las integrales singulares, las ecuaciones diferenciales aplicadas a transporte sobre filamentos, el cálculo de variaciones o las propiedades de dispersión de flujos saturados, se unen a los avances en microscopía, la comprensión de los mecanismos moleculares de la señalización celular basados en la información bioquímica y genética, y el estudio del comportamiento celular colectivo. Es apasionante observar el poder de predicción de las matemáticas cuando éstas se asientan en principios biológicos sólidos, permitiendo caminar por senderos no explorados de la ciencia y liderar nuevos descubrimientos.

Isabel Guerrero es profesora de Investigación del CSIC, Centro de Biología Molecular Severo Ochoa. Universidad Autónoma de Madrid.

Juan Soler. Catedrático de Matemática Aplicada, Universidad de Granada.

Edición y coordinación: Ágata Timón (ICMAT)

Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales, y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: "Un matemático es una máquina que transforma café en teoremas".