Buscando números primos con un ‘pequeño’ teorema

La búsqueda de los números primos ha sido un tema recurrente en toda la historia de las matemáticas. Muchísimos han sido (y son) los matemáticos que han intentado encontrar una regularidad dentro de los números primos, una fórmula que siempre devuelva números primos o un sistema de detección que nos indique si cierto número dado es primo o no.

Alguno hay infalible, como la criba de Eratóstenes, pero inoperante en la práctica. En este artículo vamos a intentarlo de otra forma, a ver dónde llegamos.

Vamos a partir del conocido como pequeño teorema de Fermat, formulado por Pierre de Fermat sobre 1636 y demostrado por primera vez por Leonhard Euler en 1736 en su trabajo Theorematum Quorundam ad Numeros Primos Spectantium Demonstratio. Dicho teorema se puede formular de la siguiente forma:

Si p es un número primo y a es un número entero positivo que no tiene factores comunes con p (es decir, a y p son primos relativos), entonces el resto de la división de a^p-1 entre p es 1. En términos de congruencias, este teorema queda así:

En principio, este teorema puede ser muy útil para descartar que un número es primo, ya que para que un cierto número n sea primo es necesario que se cumpla el pequeño teorema de Fermat para todo entero positivo a menor que el propio n.

Veamos un ejemplo. Supongamos que queremos saber si el número 413 es primo o no, y vamos a buscar ayuda en el pequeño teorema de Fermat. Tomamos un entero positivo primo relativo con 413, por ejemplo el 2, y aplicamos el test de Fermat. Si 413 fuera primo, tendríamos que 2^{413 – 1}=2⁴¹² dejaría de resto 1 al dividirlo entre 413, pero en realidad el resto de esa división es 359. Conclusión: 413 no es un número primo. Os invito a que probéis con otros números y que nos contéis vuestros resultados.

Probemos ahora con otro número. Vamos a tomar uno mucho más pequeño para no eternizarnos con las operaciones: el 17. Comencemos tomando a=2 y viendo qué nos da la aplicación del pequeño teorema de Fermat:

2^17-1=2¹⁶=65536, que al dividirlo entre 17 deja resto 1

Probemos ahora con a=3:

3^17-1=3¹⁶=43046721, cuya división entre 17 nos da, de nuevo, resto 1

Podéis probar con cualquier otro número, ya sea mayor o menor que 17, pero que no tenga factores comunes con él (por ejemplo, no valdrían ni el 51 ni el 85), y en todos los casos obtendréis resto 1.

¿Nos dice esto que 17 es un número primo? Pues…no, por desgracia no. Lo único que nos asegura esto es que no podemos descartar que 17 sea primo…

…pero sabemos que 17 sí es primo. Si probáis con cualquier otro número primo, tal y como dice el pequeño teorema de Fermat, siempre obtendréis resto 1 en las divisiones que el teorema dice que hagamos. Por esto, no sería descabellado pensar que los primos son los únicos que cumplen esta propiedad (vamos, que el recíproco del pequeño teorema de Fermat también es cierto), pero, ohhhhh, no es así.

El 561 es el menor número compuesto que pasa el test de Fermat. Es, por tanto, el primer número de Carmichael.

Hay números n que cumplen que, para todo a primo relativo con ellos, las divisiones dan siempre resto 1 sin que dicho número n sea primo. Estos números se denominan números de Carmichael, debido a que fue Robert Carmichael el que encontró el primero de ellos, el 561, en 1910.

Un número a que cumple que, para cierto n, la “división de Fermat” da resto 1 se llama testigo de Fermat. Este nombre se debe a que el hecho de que esto ocurra nos da como pista que el número n podría ser primo (aunque no nos lo asegure). Los números de Carmichael son números compuestos que cumplen que todos los números primos relativos con ellos son testigos de Fermat.

Efectivamente, 2⁵⁶⁰ deja resto 1 al dividirlo entre 561; 5⁵⁶⁰ también deja resto 1 al dividirlo entre 561; y lo mismo pasa para cualquier otro valor de a que sea primo relativo con 561, lo que nos podría llevar a pensar que 561 puede ser primo…

…pero sabemos que no lo es, y se puede ver de una manera muy sencilla: como sus cifras suman 12, que es múltiplo de 3, tenemos asegurado que 561 es múltiplo de 3, y por tanto compuesto. Vamos, que es un número con apariencia de primo (pasa el “test de Fermat”) pero que en realidad no es primo.

Como acabamos de comentar, usar el test de Fermat (o cualquier otro) para sacar alguna conclusión sobre la primalidad del número 561 es una tontería, ya que es fácil y rápido ver que es un número compuesto, pero para otros números sí nos puede venir bien para hacernos una idea sobre si son primos o no. Imaginad un número n que sea, por ejemplo, producto de dos primos de 50 dígitos cada uno. Si le pasamos el test de Fermat comenzando con los valores de a más pequeños (para que las operaciones sean lo más cortas posibles) y obtenemos siempre resto 1, ¿qué pensaríamos? Pues que es bastante probable que el número sea primo, y por eso tiene sentido que se le llame primo probable.

Pero hemos dicho que nuestro número es producto de dos números primos, y por tanto no es primo. Al ser compuesto, pasa a denominarse pseudoprimo (habría que hacer alguna puntualización al respecto de esto último, pero como no nos hace falta me la salto).

Los números de Carmichael, también llamados pseudoprimos absolutos, deben tener al menos tres factores primos (como, por ejemplo, el 561=3 · 11 · 17). Vamos, que aunque no puedan tener sólo dos factores estamos en un caso del estilo al comentado antes: son los números que hacen que no nos podamos fiar del pequeño teorema de Fermat.

Por cierto, aquí os dejo un listado con los primeros números de Carmichael (secuencia A002997 en la OEIS):

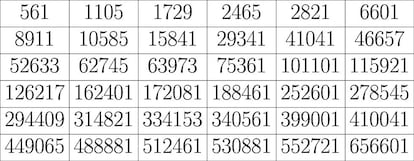
Después de todo lo que hemos comentado, ¿para qué nos podría servir entonces el pequeño teorema de Fermat? Pues, como ya hemos dicho, para detectar primos probables. Haríamos lo siguiente:

- Tomamos el número n del que queremos saber si es primo o compuesto

- Le pasamos el test de Fermat con algunos valores de a pequeños (y primos, para no perder el tiempo): 2, 3, 5, 7,…

- Si con alguno de ellos obtenemos resto distinto de 1, ya sabemos que nuestro n es compuesto.

- Si obtenemos resto 1 con todos ellos, estamos ante un primo probable. En ese caso, lo mejor es pasar a un test de primalidad más completo que el de Fermat, como el test de Miller-Rabin. En la página personal de Ben Lynn tenéis algo más de información al respecto.

Para acabar, os dejo algunos datos más relacionados con estos interesantes números de Carmichael. Son números bastantes escasos (por ejemplo, por debajo de 1000000 sólo hay 43 números de Carmichael), pero están perfectamente caracterizados. Hay un teorema, debido a Alwin Korselt y que data de 1899, que nos da condiciones necesarias y suficientes para que un número entero positivos sea un número de Carmichael:

Un número entero positivo compuesto n es un número de Carmichael si y sólo si es libre de cuadrados y para todo divisor primo p de n se cumple que p – 1 es un divisor de n – 1.

(Que un número K sea libre de cuadrados significa que no hay ningún número primo q tal que q² sea un divisor de K.)

Este teorema caracteriza totalmente a los números de Carmichael: si encontramos un número compuesto con esas condiciones tenemos asegurado que será un número de Carmichael.

Un último detalle sobre este teorema en el que puede que alguno haya reparado: el teorema de Korselt es anterior a la propia definición de número de Carmichael. Al parecer, Korselt no fue capaz de encontrar ningún número con esas características, y hubo que esperar a que Carmichael encontrar el 561 unos años después de la aparición de este teorema.

Por otra parte, tenemos otro interesante teorema, demostrado por Jack Chernick en 1939, que nos proporciona un subconjunto de los números de Carmichael. El teorema dice lo siguiente:

Un número de la forma (6k+1) · (12k+1) · (18k+1) es un número de Carmichael si sus tres factores son números primos (más información en On Fermat’s Simple Theorem).

Y, para finalizar, un apunte sobre la cantidad de estos números. Como decíamos, los números que citan el teorema de Chernick son solamente algunos de los números de Carmichael, y no se sabe cuántos hay (si son finitos o infinitos). ¿Y qué ocurre si hablamos de todos los números de Carmichael? Pues que, desde 1994, sabemos que hay infinitos números de Carmichael. Lo demostraron Alford, Granville y Pomerance en su trabajo There are infinitely many Carmichael Numbers. Son escasos, y son raros, pero son infinitos.

Como a muchos matemáticos a lo largo de toda la historia, me fascinan los números primos y todo lo que les rodea. Por otra parte, una de mis “debilidades matemáticas” es todo lo que se refiere a Pierre de Fermat. Por ello he querido hablaros sobre este pequeño teorema de Fermat y su relación con la búsqueda de números primos. Además, me ha servido para mostraros estos curiosos números de Carmichael y algunas de sus propiedades.

Sobre números primos seguiremos hablando. Y, sobre ellos, me gustaría que propusierais en los comentarios temas relacionados con ellos que puedan ser susceptibles de ser tratados en este blog. Muchas gracias.