Brook Taylor, músico, pintor, jurista y gran matemático

La llamada serie de Taylor no es tan mediática como Juego de Tronos, pero resulta fundamental en el cálculo matemático y, con ello, en el resto de ciencias e ingeniería. Su autor, el inglés Brook Taylor, tampoco es tan conocido como otros científicos, aunque cualquier estudiante de ingeniería u otras ciencias se ha enfrentado, en un inevitable curso de cálculo, a alguna de las criaturas matemáticas que llevan su nombre: la serie de Taylor, el polinomio de Taylor, la fórmula de Taylor… Sin embargo, su obra, o mejor dicho, sus intereses no se limitaron al quehacer matemático. Estudió leyes en Cambridge y recibió una sólida educación musical y artística, con varios tutores privados que se podía permitir gracias a la holgada posición económica de la familia.

Más información

Científicos en guerra: Newton, Leibniz y el cálculo infinitesimal

El irresistible encanto de las matemáticas

Hace poco más de 332 años, el 18 de agosto de 1685, nacía en Edmonton, una pequeña localidad de los alrededores de Londres, en el seno de una familia adinerada con extensas inquietudes artísticas e intelectuales. Su formación polifacética marcó una clara amplitud de miras a lo largo de su carrera. Trabajó en diversos problemas fundamentales de las artes y las ciencias: estudió el problema de la cuerda vibrante, fundamental para comprender el funcionamiento de instrumentos musicales como la guitarra o el piano, y cuya solución requería una considerable madurez matemática; desarrolló el llamado método de las diferencias finitas, que permite resolver ciertas ecuaciones diferenciales mediante un sencillo procedimiento de álgebra lineal; se interesó por temas de probabilidad, magnetismo, diseño de termómetros, y un largo etcétera. En 1715, publicó su tratado Linear Perspective que constituye uno de los primeros estudios formales sobre perspectiva y puntos de fuga.

Su vida ejemplifica la potente correlación entre juventud y creación matemática: en 1712, con tan solo 27 años, ingresó en la prestigiosa Royal Society de Londres, y, tres años más tarde, siendo secretario de esta sociedad, publicó su obra Methodus incrementorum directa et inversa, en el que presentó una de sus grandes aportaciones a las matemáticas: la serie de Taylor, que permite representar casi cualquier función de una variable como una serie (una suma infinita). Esta técnica permite aproximar muchas funciones por polinomios (sumas y restas de expresiones como ax, bx², cx³…), muy fáciles de calcular en términos de las derivadas sucesivas de la función.

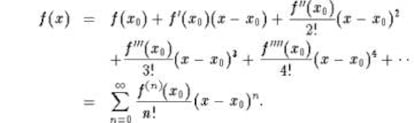
La serie de Taylor de la función es el límite de esa sucesión infinita de polinomios. Precisamente, llamamos funciones analíticas a aquellas para las que dicha serie es convergente cerca de cada punto. En la práctica, muchas funciones son analíticas, por lo que para aproximar la función basta un número finito de elementos de la serie (cuantos más términos se consideren, se tendrán mejores aproximaciones a la propia función). De hecho, el Teorema de Taylor proporciona una estimación del error que se comete con la aproximación en cada caso.

Según los historiadores, existen precursores de las series de Taylor en los trabajos de la Escuela de Kerala de astronomía y matemáticas, del sur de India, durante los siglos XIV a XVI; y en las representaciones de funciones trigonométricas descubiertas por el matemático y astrónomo escocés James Gregory en el siglo XVII. Sin embargo, no hay duda de que el primero en formalizarlo con generalidad fue Taylor, aunque su trabajo permaneció largo tiempo en el olvido, hasta que el matemático francés Joseph Louis de Lagrange lo rescatara en 1772, resaltando su importancia para el desarrollo del Cálculo Diferencial. De hecho, Lagrange, e independientemente Augustin Louis Cauchy, profundizaron en la comprensión de las series de Taylor obteniendo expresiones explícitas del error cometido en las aproximaciones, proporcionando la versión actual y más completa del Teorema de Taylor.

Por su parte, sir Isaac Newton y Gottfried Leibniz, ambos autoproclamados fundadores del Cálculo en una gran controversia durante el s. XVIII, también desarrollaron sus propias versiones de lo que hoy se conoce como Teorema de Taylor. En el comité constituido en 1712 para mediar en dicha disputa y atribuirle a cada uno lo suyo, se incluyó a un jovencísimo Taylor, muestra de la especial relevancia y conocimiento que este tenía en el campo del cálculo.

Brook Taylor falleció en Londres en 1731, a la edad de cuarenta y seis años, tras vivir una serie de tragedias familiares. No resulta difícil imaginarse su epitafio: amante de la música, pintor con talento, doctor en leyes y, en sus ratos libres, gran matemático.

Pedro Tradacete es Profesor Visitante en el Departamento de Matemáticas de la Universidad Carlos III de Madrid.

Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales, y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.