El infinito y más acá

Llamando d a la diagonal de un cuadrado de lado 1, por el teorema de Pitágoras sabemos que

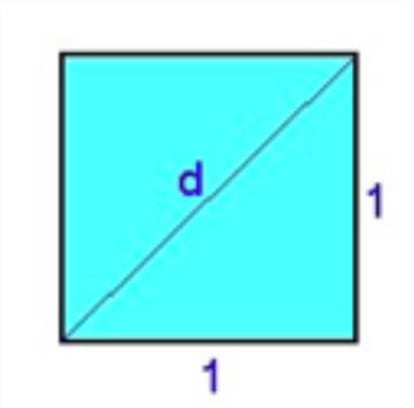
d² = 1² + 1² = 2

d = √2.

Si √2 fuera un número racional, es decir, una fracción, podríamos decir que √2 = a/b, donde a y b no son ambos pares (pues en ese caso podríamos dividirlos ambos por 2 y simplificar la fracción); por lo tanto:

2 = a²/b²

a² = 2b²

Así pues, a² es par, luego a también lo es (ya que el cuadrado de un número impar siempre es impar) y podemos escribirlo en la forma a = 2n (siendo n un número entero), de donde a² = 4n², y como a² = 2b², 2b² = 4n², b² = 2n², luego b² es par, lo que significa que b también lo es, en contra de la hipótesis de partida, según la cual a y b no son ambos pares. Por lo tanto, no existe una fracción a/b que sea igual a √2.

Y de forma tan sencilla y elegante demostró Hipaso de Metaponto, hace unos dos mil quinientos años, la existencia de los números irracionales.

Primos, libros y cuadros

Como hemos visto en las últimas semanas, el de los números irracionales es un infinito de orden superior al de los números naturales, un infinito no numerable (que es una forma de decir que sus elementos no pueden ponerse en correspondencia de uno a uno con el conjunto de los números naturales). Pero ¿qué pasa con los números primos, tan escurridizos e inquietantes como los irracionales? Si los irracionales están más allá del infinito, ¿están los primos más acá?

A medida que vamos avanzando en la sucesión de los números naturales, los primos son cada vez más escasos; de hecho, podemos encontrar dos primos sucesivos tan alejados como queramos (¿puedes demostrarlo?). ¿Significa eso que a partir de un cierto punto ya no habrá más números primos? Pues no: Euclides, que no solo fue el padre de la geometría, sino que también destacó en otras ramas de las matemáticas, demostró que hay infinitos números primos. ¿Puedes reconstruir su sencilla e ingeniosa demostración?

Y así como los primos podrían parecer finitos pero no lo son, hay finitos que no lo parecen, o cuando menos son dudosos. Por ejemplo, se suele decir que el lenguaje es infinito, pero ¿lo es realmente? ¿Es infinito el número de libros escribibles? ¿Y el número de cuadros pintables?

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’