Diagonales

Si al quitarle un elemento a un conjunto infinito A se convirtiera en un conjunto finito B, los elementos de B podrían ponerse en correspondencia de uno a uno con una sucesión finita de números naturales, digamos del 1 al n; por lo tanto, al devolverle a A el elemento quitado, podríamos ponerlo en correspondencia con los números del 1 al n+1, luego A no sería infinito.

Con todos los conjuntos finitos de números naturales podemos hacer lo mismo que hicimos con todas las parejas posibles: ordenarlos de menor a mayor según la suma de sus miembros; por lo tanto, son numerables (ver las dos columnas anteriores).

Pero si consideramos también los conjuntos infinitos, la cosa cambia. El conjunto de todos los conjuntos de números naturales, incluidos los conjuntos infinitos, se denomina “potencia de N” o P(N), donde N es el conjunto de los números naturales, y P(N) no es numerable. Raymon Smullyan lo ilustra de la siguiente manera:

Imaginemos un libro con infinitas páginas numeradas: 1, 2, 3, 4…, en cada una de las cuales se describe un conjunto de números naturales. ¿Pueden estar en el libro todos los conjuntos posibles? No, y para demostrarlo basta con encontrar un conjunto que no puede estar en el libro. ¿Se te ocurre alguno?

De lo anterior se desprende que el proyecto del empadronador del mundo de infinitos habitantes no es viable, pues dar a cada club posible el nombre de un habitante equivale a numerar el conjunto de todos los conjuntos de números naturales.

Aunque en la columna anterior no se habla de Cantor, él fue quien demostró, mediante su famoso “método diagonal”, que los irracionales no son numerables (ver Hasta el infinito y más allá), y todas las demostraciones que hemos visto luego son variantes de su método.

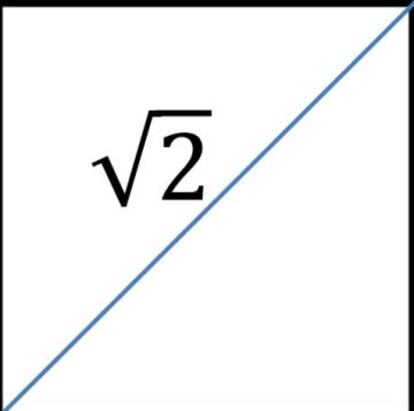
La diagonal del cuadrado

Y hablando de diagonales, la aparentemente inofensiva diagonal del cuadrado provocó, hace unos 2.500 años, una conmoción comparable a la de la diagonal de Cantor.

Los pitagóricos creían que los números que no eran enteros eran fraccionarios, o lo que es lo mismo, racionales; es decir, que se podían expresar mediante una fracción, que es el cociente o razón de dos números enteros. Pero Hipaso de Metaponto demostró que la longitud de la diagonal de un cuadrado de lado 1 no podía expresarse mediante una fracción: era un número “irracional” (en el sentido de que no es la razón de dos enteros).

La demostración de Hipaso era tan sencilla como ingeniosa, y no requería más conocimientos matemáticos que el teorema de su maestro Pitágoras. ¿Puedes reproducirla sin ayuda de internet?

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’