El tablero astronómico

EL PAÍS y Materia proponen a sus lectores, cada semana, un juego de lógica. Los lectores pueden enviar sus soluciones en los comentarios, y plantear nuevos acertijos y juegos. La respuesta correcta será ofrecida en la columna de la semana siguiente.

La recompensa que el mítico inventor del ajedrez le pidió al rey de la India constituye uno de los más conocidos ejemplos del vertiginoso crecimiento de las progresiones geométricas. Un grano de trigo por la primera casilla del tablero, dos por la segunda, cuatro por la tercera, ocho por la cuarta… La intuición nos dice que con un saco de trigo será suficiente, y sin embargo no bastaría la cosecha mundial de muchos años para suministrar los aproximadamente 18 trillones y medio de granos resultantes.

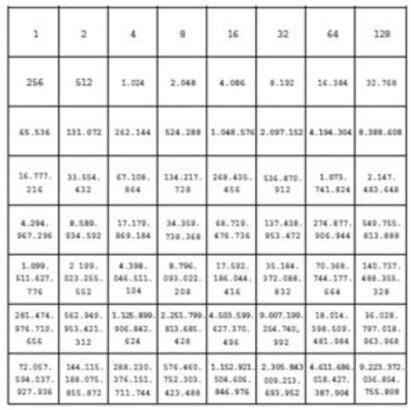
El cálculo es sencillo, sin necesidad de echar mano de las fórmulas matemáticas: basta con ver que los granos de cada casilla superan en una unidad a los de todas las anteriores juntas: 2=1+1, 4=2+1+1, 8=4+2+1+1… En la casilla 64ª, tras 63 duplicaciones, habrá 2⁶³ granos, luego en todas las anteriores juntas habrá 2⁶³-1, y en total: 2⁶³+2⁶³-1=2⁶⁴-1.

En cuanto a la torre de Hanói, hemos visto que para trasladar tres discos (numerados de menor a mayor: 1, 2 y 3) son necesarios un mínimo de siete movimientos, siguiendo la secuencia 1213121. Ahora bien, para dos discos la secuencia es 121, o sea, que lo que hemos hecho ha sido trasladar una torre de dos discos, luego desplazar el tercer disco y por último volver a trasladar la torre de dos discos para ponerla encima del tercero. Es fácil comprobar que, análogamente, con cuatro discos la secuencia es 121312141213121: primero trasladamos una torre de tres discos, luego desplazamos el cuarto, y por último volvemos a trasladar la torre de tres para ponerla encima del cuarto disco. Y así sucesiva e indefinidamente.

Así pues, a medida que aumenta el número de discos, el número de movimientos necesarios para trasladarlos crece según la progresión 1, 1+1+1=3, 3+1+3=7, 7+1+7=15, 15+1+15=31… Pero 1, 3, 7, 15, 31… son las sucesivas potencias de 2 menos 1; por lo tanto, para trasladar una torre de 64 discos harán falta 2⁶⁴-1 movimientos, tantos como granos de trigo le pidiera al rey de la India el inventor del ajedrez.

Un número astronómico, sin duda, pero ni mucho menos el mayor de los que pueden proliferar en un damero. Consideremos, sin ir más lejos, el número de jugadas posibles en una partida de ajedrez. En su primera jugada, las blancas tienen 20 opciones (adelantar una o dos casillas cada uno de los ocho peones y mover cada caballo a una de las dos casillas accesibles), y a cada apertura pueden responder las negras, asimismo, de 20 maneras distintas, con lo que tenemos 400 combinaciones posibles. Tras el segundo movimiento de las blancas, las situaciones posibles son ya más de 5.000, y más de 70.000 tras el segundo movimiento de las negras (exactamente 72.084). Tras el tercer movimiento de las blancas hay más de 800.000 posiciones posibles, y más de 9.000.000 tras el tercero de las negras… Si siguiéramos adelante, llegaríamos a una cifra del orden de los septillones, frente a la cual los 18 trillones y medio de granos de trigo del inventor del ajedrez se convierten en una insignificante migaja.

Pero volvamos a los números abarcables: acabamos de ver que las situaciones posibles tras el segundo movimiento de las blancas son más de 5.000, pero… ¿cuántas son exactamente?

Y hablando de las primeras jugadas del ajedrez, ¿cuál es la partida más corta posible?

Carlo Frabetti

Escritor y matemático, miembro de la Academia de Ciencias de Nueva York, ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’