Criptografía: las matemáticas que hacen segura la mensajería instantánea
El protocolo empleado por WhatsApp hace uso de conceptos como las curvas elípticas, el logaritmo discreto elíptico y la aritmética modular

La popular aplicación de mensajería instantánea WhatsApp garantiza la seguridad de sus mensajes gracias a un sistema de cifrado denominado de extremo a extremo. Con este método, en el que el cifrado y descifrado de los mensajes se realiza en el teléfono móvil de los usuarios y, además, las claves de cifrado se renuevan con cada mensaje, se puede asegurar que, salvo los receptores, nadie, ni siquiera la propia app, pueda leer las comunicaciones. Para ello se hace uso de conceptos matemáticos como las curvas elípticas, el logaritmo discreto elíptico y la aritmética modular.
El sistema que emplea WhatsApp es simétrico, es decir, utiliza la misma clave para cifrar y descifrar los mensajes —en contraposición, los asimétricos usan claves de cifrado y de descifrado diferentes—. Los simétricos requieren menos recursos informáticos y son más fáciles de utilizar, pero en ellos es fundamental garantizar la seguridad de la clave común que comparten dos interlocutores. Esta clave se genera intercambiando información por un canal público, utilizando el método introducido por Whitfield Diffie y Martin Hellman en 1976. El reto para implementarlo reside en diseñar algoritmos —o funciones— de una sola dirección, es decir, fáciles de ejecutar, pero que, a partir del resultado, no sea posible —computacionalmente— averiguar el punto de partida.
Para crear una clave secreta común, cada interlocutor elige un número, que mantiene secreto —será la clave privada— y, a partir de él, mediante una función de una sola dirección, produce su propia clave pública. Después, cada uno realiza por su cuenta los mismos cálculos, partiendo de la clave privada propia y de la pública de su interlocutor, de manera que los dos obtienen un mismo número, la clave común.
En 1985, Neal Koblitz y Victor Miller propusieron, independientemente, utilizar métodos Diffie-Hellman basados en los puntos de un tipo de curva llamada elíptica. La ventaja de esta opción es que las claves son relativamente pequeñas —solo ocupan 256 bits— y son fáciles de ejecutar.
En particular, WhatsApp utiliza la llamada curva elíptica de Montgomery Curve25519, introducida por Daniel J. Bernstein en 2005, que tiene como ecuación y² = x³ + 486662x² + x.
Las operaciones matemáticas se realizan en aritmética modular. En concreto, en los puntos de la curva elíptica se define una suma, que viene explicada en la imagen posterior. A partir de ella, se determina la “suma d veces” de un punto P —que se denota dP—, que es la función de una sola dirección que permite obtener las claves comunes seguras en las que se sustenta el cifrado.
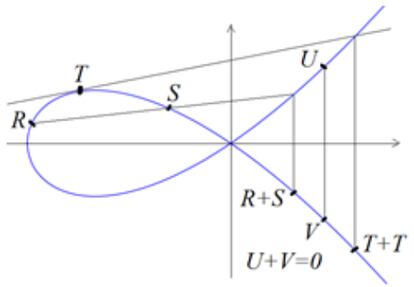
Para ello, los dos interlocutores —llamémosles Ander y Beatriz— eligen su número secreto —d1 y d2, respectivamente—. Cada uno calcula su clave pública sumando el punto base P elegido las veces dadas por su número secreto —el resultado de Ander es d1P y el de Beatriz, d2P—. A continuación, con su clave privada y la pública de Beatriz, Ander calcula d1(d2P) y, por su lado, Beatriz calcula d2(d1P). Los dos obtienen el mismo resultado (la operación dP es conmutativa), que es la clave secreta común. Como decíamos, la seguridad del método reside en garantizar que de un resultado dP no sea posible obtener computacionalmente el número d que lo ha generado, es decir, en que sea una función de una sola dirección. Este el llamado problema del logaritmo discreto elíptico.
Una vez disponible la clave común, con WhatsApp se cifran y descifran los mensajes en el propio teléfono móvil. En concreto, esto se hace con el sistema criptográfico simétrico Advanced Encryption Standard —que es una versión del algoritmo Rijndael para claves de 256 bits, propuesto en 1998 por Vincent Rijmen y Joan Daemen—. Con la potencia informática actual, es prácticamente irrompible.
Además, los interlocutores de WhatsApp generan y renuevan, con cada mensaje, la clave común de cifrado y descifrado, lo que aumenta aún más la fiabilidad del sistema. Para cada envío de una tanda de mensajes, el usuario genera en su móvil un par de claves privada-pública y, con su clave privada y la pública del destinatario, calcula la clave raíz común. A partir de ella, genera automáticamente, de forma encadenada, una subclave diferente para cifrar cada mensaje. En la cabecera de los mensajes incluye su clave pública. El destinatario calcula la misma clave raíz y, con ella, obtiene las subclaves y descifra los mensajes. Para sus respuestas hace lo mismo y cuando quien empezó la comunicación las recibe, renueva las claves privada-pública y replican el proceso cuantas veces quieran. Así, con cada tanda de mensajes se renueva la clave raíz y las subclaves de mensaje.
Otras aplicaciones de mensajería instantánea, como Signal, también utilizan un sistema de cifrado extremo a extremo para proteger todas las comunicaciones, pero no todas funcionan de esta manera. Por ejemplo, Telegram tiene una opción de cifrado con su propio protocolo llamado MTProto. En ella, la aplicación no guarda los mensajes localmente, sino que los guarda en la nube.
Mikel Lezaun es catedrático de Matemática Aplicada de la Universidad del País Vasco (UPV/EHU).
Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.
Edición y coordinación: Ágata A. Timón G Longoria (ICMAT).
Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.
Archivado En
- Ciencia
- Informática
- Computación
- Computación en nube
- Ciencia y Tecnología Aplicada
- Criptografía
- Algoritmos computacionales
- Apps
- Aplicaciones informáticas
- Inteligencia artificial
- Matemáticas
- Ciencias exactas
- Tecnología
- Identificacion
- Computación cuántica
- Automatización
- Privacidad internet
- Seguridad internet
- Seguridad personal
- Informáticos
- Información privilegiada
- Alan Turing
- Mensajería
- Tecnología digital
- Café y teoremas
- Números información telefónica
- Máquina Enigma




























































