Los misterios de la cicloide, una de las curvas más presentes en la naturaleza

Tal día como hoy, 19 de junio, hace 400 años, nacía el matemático, físico, filósofo, teólogo e inventor Blaise Pascal en Clermont (Francia). El delicado estado de salud en el que vivió toda su vida no le impidió realizar numerosas contribuciones en geometría, probabilidad, combinatoria y mecánica de fluidos. En honor a sus contribuciones en esta última área, la unidad de medida de presión en el Sistema Internacional de Unidades se conoce como pascal. Además, aunque son menos populares, también realizó profundas aportaciones sobre una de las curvas más presentes en la naturaleza: la cicloide. Sus ideas se anticiparon unos pocos años al desarrollo del cálculo infinitesimal, una teoría fundamental en las matemáticas modernas y sus aplicaciones.

Pascal no asistió a ningún colegio ni universidad, pero su padre le enseñó latín, griego, matemáticas, historia, filosofía y derecho canónico y civil. Desde una temprana edad mostró talento en matemáticas y se formó con los Elementos de Euclides de manera autodidacta. Con tan solo 19 años comenzó a diseñar una calculadora mecánica, conocida como pascalina, con el fin de ayudar a su padre en su puesto de recaudador de impuestos.

Fue en sus últimas contribuciones en matemáticas, recogidas en su correspondencia con Pierre de Carcavi —matemático y secretario de la Biblioteca Nacional francesa durante el reinado de Luis XIV—, cuando se centró en una curva llamada cicloide. La cicloide es la curva descrita por un punto de una circunferencia cuando esta rueda sobre una recta sin resbalar. Es decir, si tenemos una rueda y marcamos un punto en su borde, al hacer rodar la rueda a lo largo de una recta, el punto señalado trazará una cicloide.

Como el propio Pascal dijo, la cicloide es, junto con la línea recta y la circunferencia, una de las líneas más comunes en la naturaleza. Así, se encuentra en las crestas de la superficie helada de Europa, el satélite de Júpiter. Los arcos en forma de cicloide se emplean en arquitectura; de hecho, este es el motivo por el cual el célebre Galileo Galilei se interesó en conocer su área. Asimismo, ciertas máquinas emplean reductores cicloidales, unos engranajes cuyo contorno tiene forma de cicloides.

No está claro quién fue la primera persona en describir la cicloide. La primera mención a la cicloide se asocia a Charles de Bovelles, en 1501; pero —tal y como afirma el matemático e historiador Paul Tannery—, “en la curva de doble movimiento de Carpo [de Antioquía] es difícil no reconocer la cicloide, cuya generación tan simple no pudo escapar a los antiguos”.

Los primeros estudios publicados sobre las propiedades de la cicloide son de Galileo. En concreto, realizó una estimación del área que encierra la curva de forma experimental: generó una cicloide haciendo rodar un disco de metal, fabricó una pieza del mismo metal con la forma del área bajo dicha cicloide y comparó los pesos del disco y de dicha pieza. Su resultado —3π por el cuadrado del radio del disco— fue demostrado, de manera independiente, por Pierre de Fermat y Gilles de Roberval.

Pero Pascal se dio cuenta de que es interesante conocer las propiedades no solo de la cicloide completa, sino también de sus arcos, y del área y volumen que estos encierran. Fue capaz de determinar el área y centro de gravedad de la figura plana encerrada por un arco de cicloide —en la figura inferior se corresponde con la parte sombreada—. Además, calculó los volúmenes y centros de gravedad de las figuras tridimensionales que se generan haciendo girar esta figura plana alrededor de su eje vertical u horizontal.

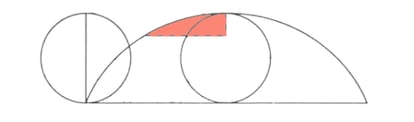
Para ello, Pascal hizo uso del método de indivisibles, que ya usaban los antiguos griegos. Este método se basa en considerar a las líneas como “sumas” de puntos, a las figuras planas como “sumas” de líneas y a las figuras tridimensionales como “sumas” de figuras planas. Estas ideas fueron refinadas unos años más tarde por Isaac Newton y por Gottfried Wilhelm Leibniz, en sus desarrollos del cálculo infinitesimal.

Sus resultados sobre la cicloide y otras de sus muchas contribuciones a diferentes áreas están explicadas de forma cronológica por el historiador y escritor Donald Adamson en Blaise Pascal: Mathematician, Physicist, and Thinker about God. Efectivamente, además de realizar brillantes contribuciones en matemáticas y filosofía, realizó importantes experimentos en física, que llevarían a la invención de la prensa hidráulica o la jeringa. La trayectoria de Pascal, y la historia de la cicloide, son una muestra de cómo el conocimiento teórico y práctico son inseparables.

Asier López Gordón es investigador predoctoral en el Instituto de Ciencias Matemáticas (ICMAT)

Ágata A. Timón García-Longoria es coordinadora de la Unidad de Cultura Matemática del ICMAT

Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.

Edición y coordinación: Ágata A. Timón G Longoria (ICMAT).

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.