
La geometría como emblema de la razón
¿Constituyen las matemáticas un lenguaje universal comprensible para cualquier criatura inteligente?

¿Constituyen las matemáticas un lenguaje universal comprensible para cualquier criatura inteligente?
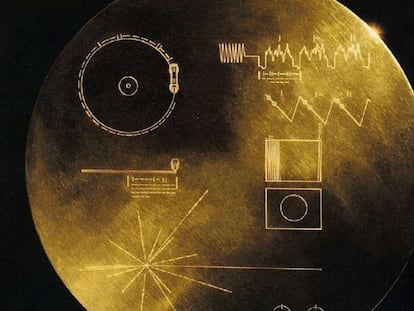
Un profesor de inglés concibió en 1960 un “mensaje interplanetario” con 24 símbolos aún sin descifrar

El físico estadounidense Gerard K. O'Neill propuso la construcción de colonias espaciales en forma de enormes estructuras giratorias orbitando alrededor de la Tierra

Las fábulas de Stanislaw Lem suponen una aproximación a la vez humorística y filosófica al universo de los robots

¿Cumplirán los robots reales, que ya están entre nosotros, las tres leyes de la robótica de Asimov?

En su saga de las Fundaciones, Isaac Asimov imagina una civilización humana diseminada por toda la galaxia

Podría haber tres grandes tipos de civilizaciones galácticas, según su nivel de aprovechamiento energético

Para aprovechar al máximo la energía de su estrella, una civilización avanzada podría construir una gigantesca “cáscara” a su alrededor

Si un astronauta viaja a Alfa Centauri a gran velocidad y regresa, ¿será más joven que su hermano gemelo, que permaneció en la Tierra?

¿Existe realmente este siniestro lugar evocado por un conocido poema?

¿Por qué si hay tantos planetas susceptibles de albergar vida inteligente, ninguna civilización extraterrestre se ha puesto en contacto con nosotros?

¿Cuántas civilizaciones capaces de comunicarse con nosotros hay en la Vía Láctea?

Fermi era famoso por su habilidad para hallar soluciones muy aproximadas a partir de datos insuficientes. ¿Puedes emularlo?

¿Qué ocurre si, en una liga de fútbol, se incorporan equipos que no estuviesen previstos?

Hay muchas variantes del dominó, y partir de las más elementales ayuda a comprender su compleja combinatoria
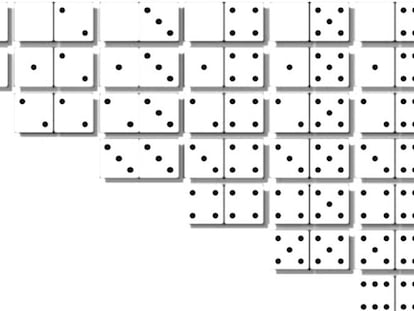
¿Cuántas cadenas distintas se pueden formar con las 28 fichas de dominó?

¿Cuántas banderas de tres franjas se pueden formar con seis colores?
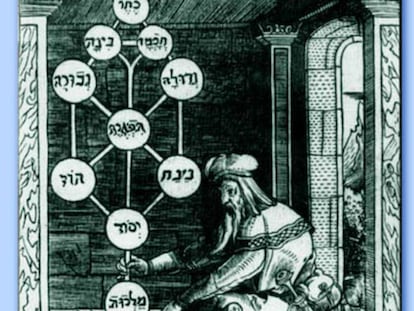
Girona fue un importante centro cabalístico, lo que invita a especular sobre la combinatoria de las letras de su nombre

¿De cuántas maneras distintas pueden combinar los monjes tibetanos las letras de su alfabeto en su búsqueda del verdadero nombre de Dios?

¿De cuántas maneras distintas pueden salir a pasear las nueve musas en grupos de tres sin repetir compañeras?

¿Por qué es tan contundente y “redondo” el número 100?

El gran naturalista francés Georges Louis Leclerc, conde de Buffon, hizo también importantes contribuciones a las matemáticas

No hay muchas mujeres expertas en matemática recreativa; pero al menos una, Angela Foxx Dunn, se ha ganado un puesto junto a los mejores

El problema del mono y los cocos tiene un antecedente (o dos) en el famoso libro de Malba Tahan

¿Podría un mono muy listo, como la gorila Koko, resolver el problema del mono y los cocos?

Demostrar que hay al menos dos comentaristas de 'El juego de la ciencia' que tienen el mismo número de colegas en la sección de comentarios

¿Es correcta la más famosa afirmación del genial matemático indio Srinivasa Ramanujan?

El teorema de Banach-Tarski demuestra que podemos trocear una esfera y reagrupar sus fragmentos para obtener dos esferas iguales a la original

No solo los héroes mitológicos sino también los matemáticos se enfrentan a tareas sobrehumanas

En tu álbum de fotos familiar hay un pez, te advierte Richard Dawkins en su libro 'La magia de la realidad'

¿Hasta dónde podemos llegar trepando por nuestro árbol genealógico?

“Cierto es el testimonio de uno de ellos que afirma que los cretenses mienten siempre”, dijo San Pablo

Números que se resisten a ser definidos, narices que solo pueden crecer si no crecen…

Los números, como los objetos, se definen mediante palabras, lo cual puede dar lugar a extrañas contradicciones

Los números son palabras, las palabras son figuras, las figuras son números…

¿Qué eres capaz de hacer con el título de este artículo, que en realidad es un desafío mental en sí mismo?

De cómo un anagrama de Galileo llevó a Kepler a “descubrir” los satélites de Marte, también descubiertos por los laputienses de Swift

En la mayoría de los juegos las reglas se conocen de antemano, pero en el juego de la ciencia no es así

A las máquinas les resulta más fácil emular las capacidades intelectuales de los humanos que sus habilidades motrices

¿En qué se parecen un cuervo y un pupitre?, le pregunta a Alicia el Sombrerero Loco