Así sería la ciudad de Dido

Mari Luz García Escamilla, gestora del Posgrado en Matemáticas de la Universidad Autónoma de Madrid, resuelve el segundo desafío matemático que este verano planteamos a nuestros lectores (puede ver aquí el vídeo). Una vez realizado el sorteo entre las respuestas correctas, de las 730 recibidas, el ganador de la colección de libros Grandes Ideas de la Ciencia ha sido Raúl Sáez, quien trabaja como analista de información en una compañía de seguros y reside en Alcobendas (Madrid).

Para evitar confusiones y en atención también a nuestros lectores sordos incluimos la solución por escrito a continuación:

La respuesta es que Dido debe colocar la cuerda formando un arco de circunferencia y, dado que 45° es un octavo de 360°, el arco será un octavo de circunferencia. Primero vamos a argumentar por qué ésta es la mejor solución y después calcularemos el área del sector circular.

Si pudiésemos colocar la cuerda de otra forma distinta al arco de circunferencia de forma que abarcásemos una área mayor, reflejando la superficie tres veces como muestra la figura de abajo tendríamos una cuerda que abarca una superficie mayor que la del semicírculo en las condiciones del problema de Dido simplificado que poníamos como ejemplo, lo cual es imposible.

Para calcular el área, empezamos por calcular el radio R del octavo de circunferencia. Recordemos que la longitud de la cuerda es un kilómetro, como muestra esta figura

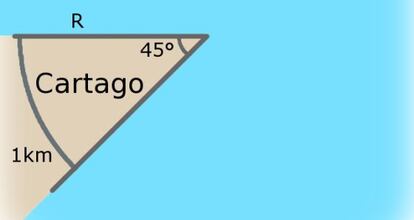
Por tanto, teniendo en cuenta la fórmula para calcular el perímetro de una circunferencia, tenemos que

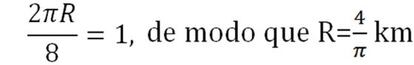
Una vez conocido el valor del radio, ya podemos calcular el área del sector circular. Así, el área máxima de la ciudad que Dido podría haber construido en el cabo es de

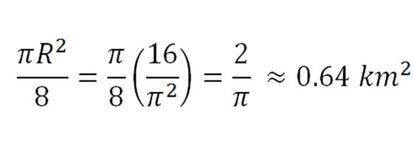
Y esa es la solución que buscábamos: la ciudad que construiría Dido tendría un área aproximada de 0,64 kilómetros cuadrados.