Una solución a la parrilla

Adolfo Quirós, vicepresidente de la Real Sociedad Matemática Española, profesor de la Universidad Autónoma de Madrid y coordinador de esta sección; resuelve el primer desafío matemático que este verano planteamos a nuestros lectores (puede ver aquí el vídeo). El ganador de la colección de libros Grandes Ideas de la Ciencia ha sido Guillermo Vicente, un ingeniero aeronáutico de Sabadell que lleva ya unos años afincado en Torrelodones (Madrid).

Para evitar confusiones y en atención también a nuestros lectores sordos incluimos la solución por escrito a continuación:

Consideremos primero las reglas ACB. Se pueden cambiar los valores de todas las casillas de una fila, de una columna, o de una de las dos diagonales. Cualquiera de estos movimientos cambia el signo en 4 casillas, de modo que si empezamos con una cantidad impar de -1, y por tanto con el producto de todas las casillas igual a -1, ese producto seguirá siendo -1 después de cualquier movimiento. Por tanto ni a partir de la parrilla 'a' ni a partir de la 'b' podemos llegar a tener un 1 en todas las casillas.

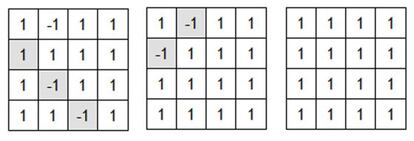
Con las reglas NBA, donde también podemos cambiar los valores de todas las casillas de una recta paralela a una de las dos diagonales, el número de cambios puede ser par o impar. De hecho empezando en la parrilla 'a' se puede ganar en dos pasos, indicados en las casillas sombreadas de esta figura:

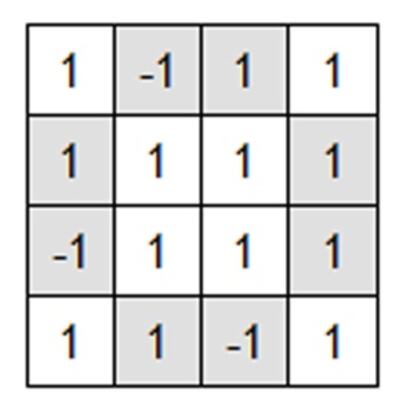
Sin embargo, si empezamos en la posición b y nos fijamos en las casillas sombreadas (ver figura de abajo) podemos observar que cualquiera de los movimientos permitidos por las reglas NBA cambia un número par (ninguna o dos) de estas casillas. Y como en ellas hay tres -1 no se puede ganar a partir de la parrilla 'b'.