Un cuadrado de 20 coches en cada lado
El problema de esta semana solo admitía una solución.- El ganador de una biblioteca matemática es Luis Alonso Albir, de Madrid, que ha mandado su solución desde la Guayana Francesa
Ya hay solución para el duodécimo desafío matemático con el que EL PAÍS celebra el centenario de la Real Sociedad Matemática Española. Josefa Ramírez Rodríguez, licenciada en matemáticas por la Universidad de Extremadura y responsable de Sistema de Información en el RACC planteó el problema (ver vídeo de la izquierda) y lo resuelve ahora (vídeo de la derecha): en la exhibición de coches participarán 400 vehículos, que en principio formaban un cuadrado de 20x20 y que terminarán formando un rectángulo de 25x16 automóviles. La solución es única, tal y como cuenta Josefa en el vídeo de la derecha y como demostraremos a continuación (porque esta semana sí estaba claro que había que justificar la respuesta).
El ganador de una biblioteca matemática como la que entrega cada semana EL PAÍS ha sido en esta ocasión Luis Alonso Albir, de Madrid, que nos escribe nada menos que desde la Guayana Francesa. Aprovechamos este detalle para recordar que aceptaremos respuestas procedentes de cualquier lugar del mundo. Eso sí, aunque las matemáticas tienen un lenguaje universal, preferimos que la explicación se envíe en castellano, pues hemos tenido serios problemas para entender otros idiomas (pero si la entendemos y es correcta también entraría en sorteo, ojo). Este domingo, en el quiosco, por 9,95 euros con el periódico, La certeza absoluta y otras ficciones, de Pere Grima
Nuestra demostración es la siguiente. Vamos a suponer que n es el número de vehículos en cada lado del cuadrado incial, n+5 el número de vehículos en uno de los lados del rectángulo final y k el número de vehículos en el otro lado del rectángulo.
Si n^2 = (n+5) k, entonces n+5 divide a n^2 pero como claramente n+5 divide a (n+5)(n-5) = n^2 -25, necesariamente n+5 ha de dividir a 25 = n^2 -(n+5)(n-5) y, como los únicos divisores de 25 son 1, 5 y 25, se deduce que necesariamente n+5 = 25 y, por tanto, n = 20. Es decir, podemos afirmar con total seguridad que participarán 400 coches. Es más, se puede ver que n+5 divide a n^2 si y sólo si n+5 divide a 25.
Esta demostración tan sencilla, nos indica que si, en lugar de 5, hubiéramos pedido que se aumentara en un número primo p de filas, la respuesta hubiera sido que sí se puede decir con total seguridad que participarían (p^2 -p)^2 coches, mientras que si hubiéramos dicho que se aumentara en un número K que no es primo la respuesta hubiera sido que no se podía decir con total seguridad, pues el número de posibilidades que tendríamos serían el número de divisores de K^2 mayores estrictamente que K, ya que bastaría con que n+K fuera divisor de K^2 y el número de éstos es mayor que 1.
Hemos querido, no obstante, dar una demostración (larga) que pensamos podían intentar nuestros lectores y que daba la clave sobre qué es lo que tenían que probar. También podríamos haber optado por realizar la división n^2 /(n+5) y habríamos obtenido k = n^2 /(n+5) = n-5 + 25/(n+5) de donde claramente se obtiene que n+5 ha de dividir a 25. Equivocadamente pensamos que la división de polinomios no sería el camino que se seguiría, pero ésta ha sido la solución elegida por un 10% de los acertantes. ¡Enhorabuena!
Se han recibido 1.865 respuestas de las cuales un 60% aproximadamente han sido correctas. De las incorrectas, el 90% han acertado la solución de 400 coches pero no han demostrado que solo hay una solución (o bien no lo han intentado o bien la demostración que dan no es correcta) por lo que no han entrado en sorteo.
De las soluciones correctas, la opción más elegida (un 60% de los acertantes) ha sido la siguiente:
Si n^2 = (n+5)(n-j), se tiene que 5j = n(5-j) y, por tanto, n = 5j/(5-j). Luego, j sólo puede ser 1, 2, 3 ó 4. Substituyendo estos 4 valores se ve que la única solución que da n un número natural es j = 4.
Esta demostración ha sido muy sencilla debido a que 5 es un número muy pequeño y, aunque no permite visualizar de forma inmediata que la propiedad importante en 5 es la de ser un número primo, sí demuestra que, a veces, un cambio en la notación (k = n-j) simplifica los cálculos.
Aquellos concursantes que han optado por el camino largo expuesto en nuestra primera opción, o bien han cometido un error que les ha llevado a concluir que no se podía decir con total seguridad el número de coches que participaban en la exhibición, o bien han optado por otra demostración larga y que consiste en resolver la ecuación de segundo grado resultante n^2 -nk-5k = 0, lo cual les ha llevado a tener que demostrar cuándo k satisface que k (k+20) es un cuadrado perfecto. En la mayoría de los casos, han probado que k = 16 lo satisface pero no han sabido probar la unicidad (la solución única), salvo en casos excepcionales como precisamente el ganador del concurso Luis Alonso Albir o, por ejemplo, Paula González Gómez o Alfonso Jesús Población Sáez, que lo han probado de una forma muy elegante.
Finalmente, en este problema ni los ficheros Excel, ni los programas informáticos que buscan los números n tales n^2/(n+5) es un número natural sirven para probar la unicidad de la solución aunque se programen hasta n = 1.000 como nos dice un concursante y se argumente que con eso basta, pues no hay ningún sitio donde se pueda hacer una exhibición de 1.000.000 coches, lo cual, aunque totalmente cierto y nos hace sonreír, no podemos darlo por correcto.
Queremos enviar, por último, muchos ánimos a Jesús González Santos para que consiga que sus hijos se interesen por la matemáticas. El próximo jueves tendrá una nueva ocasión para instruirlos con nuestro decimotercer desafío.
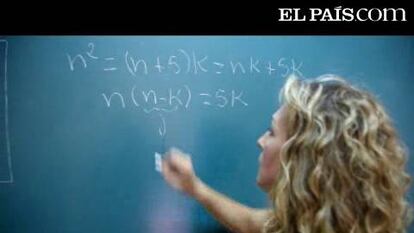

Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.




























































