¿Es posible ser 1/3 español?

Cuando iba al instituto, un profesor de matemáticas nos propuso una pregunta aparentemente inofensiva: "¿es posible ser un 1/3 español?". Está claro que cuando solo uno de los progenitores es español, su descendencia tiene 1/2 de origen español. Si solo uno de sus cuatro abuelos es español, el nieto tiene 1/4 de herencia española. ¿Pero es posible ser exactamente 1/3 español? Años después, me encontré con la misma pregunta formulada como un problema hidrodinámico denominado "problema del divisor simple". El famoso matemático Vladimir Arnold (Odesa 1937, París 2010), mi director de tesis en aquel entonces, lo estudió en uno de sus libros.

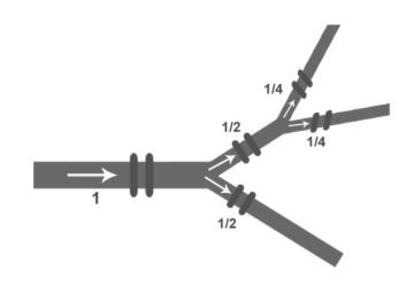
Arnold analizó el problema desde el punto de vista de la dinámica de fluidos: tenemos un río con un flujo constante de agua igual a 1 m³ de agua por segundo, y un dispositivo llamado divisor simple que permite dividir el cauce en dos corrientes iguales. Aplicando el divisor bifurcamos el río en dos riachuelos más pequeños con flujos de 1/2 cada uno; si uso otro divisor simple en cada uno de ellos, obtengo corrientes de 1/4 del flujo inicial. La pregunta es: ¿se puede usar un número finito de divisores simples para conseguir separar un arroyo cuyo flujo sea 1/3 del inicial?

Este problema, según contaba Arnold, surgió en los simulacros de defensa civil en el metro de Moscú, ya que querían dirigir a la multitud hacia tres refugios nucleares iguales. Para ello, necesitaban dividir el flujo de gente mediante torniquetes, que enviaban a una persona a la derecha y la siguiente a la izquierda (bifurcando la cola en dos grupos iguales). Como con el flujo del río, buscaban separar el grupo inicial en tres iguales, pasando por sucesivos torniquetes.

Otra manera de formular la cuestión es la siguiente: tres ladrones quieren dividir su botín, sorteando cada objeto mediante una lotería que ofrezca a cada uno la misma probabilidad de ganar (1/3), pero solo tienen una moneda, así que quieren hacerlo jugando a cara y cruz. ¿Pueden crear un sorteo justo con este método? ¿Ves la analogía entre este problema y el de dividir el río en tres cauces iguales?

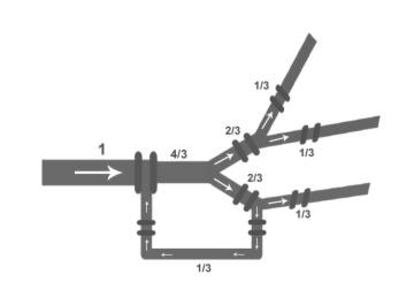
Para resolverlo, algunas personas sugirieron una solución asintótica, es decir, dividir el flujo infinitas veces de manera que el flujo de alguno de los riachuelos converge a 1/3. Pero ni para el caso de los ladrones, ni las personas del metro, ni el río, ni para las familias, nos valen infinitas divisiones. Hay otra respuesta mucho más simple. Se divide el río en cuatro cauces iguales (aplicando una vez el divisor, y en cada uno de los dos obtenidos, usando otro más), y uno de ellos se reconduce de nuevo a la corriente principal. Los tres restantes son complemente iguales, y cada uno tiene un flujo igual a un tercio del original. Para conseguir cualquier fracción del flujo se puede usar esta misma idea, simplemente dividiendo en más riachuelos, y retornando al cauce inicial los que sean necesarios

Para los tres ladrones, esta solución significaría seguir el siguiente método para rifar cada elemento de su botín: en primer lugar, se lanza la moneda dos veces; si se obtienen dos caras, el primer ladrón gana el artículo; si son primero una cara y luego una cruz, gana el segundo ladrón; si son primero cruz y luego una cara, gana el tercer ladrón; si el resultado son dos cruces, comienza de nuevo el sorteo.

Esta respuesta no sirve para el problema del refugio antiaéreo, porque algunas personas quedarían atrapadas en un bucle y nunca llegarían a los búnkeres. Y ni siquiera me atrevo a detallar qué implicaciones de endogamia y viajes en el tiempo tendría este método para obtener un origen de 1/3 español. Prefiero daros una respuesta con truco: ¡Sí, uno puede ser 1/3 español, si sus dos progenitores son 1/3 españoles!

Boris Khesin es catedrático de Matemáticas en la Universidad de Toronto (Canadá)

Traducción: Ágata A. Timón

Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: "Un matemático es una máquina que transforma café en teoremas".

Edición y coordinación: Ágata Timón (ICMAT).

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aquí a nuestra newsletter