El problema de distinguir dos fórmulas químicas iguales

En matemáticas y en química se usan fórmulas. Una fórmula matemática relaciona constantes y variables a través de una igualdad; mientras que una química, busca determinar un compuesto a partir de los átomos que contiene y la proporción en la que éstos aparecen. El gran problema radica en que distintas sustancias pueden tener la misma fórmula química, como observó en 1811 Joseph Louis Gay-Lussac. ¡Vaya! Esta fórmula, entonces, no parece demasiado útil. En 1823, el químico Justus von Liebig demostró que el fulminato de plata y el cianato de plata, ambos formados por moléculas que contenían un átomo de plata, uno de carbono, uno de oxígeno y otro de nitrógeno, tenían propiedades muy distintas: en particular, el primero era muy explosivo y el segundo no. Si sus moléculas constaban de los mismos átomos y en la misma cantidad, la diferencia entre ambos tenía que residir necesariamente en la manera en que esos átomos se enlazaban en cada molécula. Gay-Lussac comunicó estos estudios al también químico Jöns Jacob von Berzelius. De hecho, este último ya había observado un fenómeno similar: había descubierto que el ácido racémico y el ácido tartárico parecían tener la misma fórmula empírica (G4H6O6) pero no compartían las mismas propiedades.

Berzelius sugirió denominarlos isómeros. Es decir, dos compuestos químicos se llaman isómeros si poseen la misma fórmula química (mismas proporciones relativas de los átomos que componen sus moléculas) pero con diferentes estructuras químicas (maneras en que sus átomos se enlazan) y, por lo tanto, diferentes propiedades y configuración.

En 1875, el matemático Arthur Cayley, notable polímata e interesado desde joven por la química, se enteró del problema de la enumeración de los isómeros a través de su amigo, el químico alemán Carl Schorlemmer. Cayley decidió utilizar sus conocimientos sobre la teoría de grafos para enumerar todas las posibles configuraciones de los isómeros de los alcanos de fórmula CnH2n+2. Para abordar el problema empleó unos objetos matemáticos llamados grafos.

Un grafo es un conjunto formado por vértices y aristas, que representan relaciones binarias, las posibles uniones, entre los primeros. La valencia de un vértice es el número de aristas incidentes al vértice. En concreto, Cayley empleó un cierto tipo de grafos, los llamados árboles, aquellos en los que dos vértices cualesquiera están conectados por exactamente un camino de aristas.

A Cayley se le ocurrió que los vértices de los árboles podían representar los átomos de carbono de los alcanos (los de hidrógeno se podían añadir más adelante) y se trataba entonces de enumerar todas las posibles configuraciones, es decir, todos los posibles enlaces entre esos vértices. Su propuesta se basaba en el número de centros (vértices de valencia mayor que 1) de la fórmula química. Cayley demostró que estos árboles tienen siempre vértices de valencia menor o igual a cuatro y solo podían tener uno o dos centros.

Por ejemplo, consideremos dos isómeros del alcano con cinco átomos de carbono, el pentano, de fórmula C5H12. En primer lugar, el 2,2-dimetilpropano (C(CH3)4), que posee cuatro vértices de valencia 1 y uno de valencia 4, que es por lo tanto su único centro:

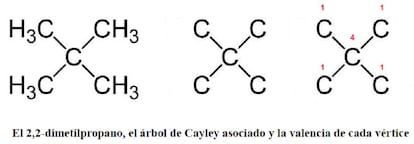
Por otro lado, el 2-metilbutano ((CH3)2-CH-CH2-CH3), que posee tres vértices de valencia 1 y dos de valencia 2; estos dos últimos son los centros:

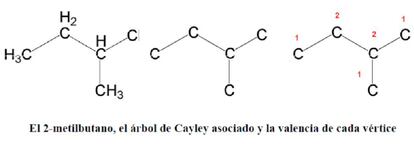
Basándose en las propiedades matemáticas de este tipo de árboles, Cayley propuso una fórmula para calcular el número de isómeros de los alcanos CnH2n+2: su expresión era exacta para n de 1 a 11, pero fallaba más allá. Una lástima.

También inventó un algoritmo que permitía calcular el número de isómeros para n (CnH2n+2) conociendo el número de isómeros para n-1 (Cn-1H2n).

Para mostrar el interés práctico de su propuesta, Cayley aplicó su método a los alcoholes de fórmula CnH2n+1OH, en los que se sustituía un átomo de hidrógeno por el radical OH. Aplicaba su teoría utilizando como vértices del árbol los átomos de carbono y el radical OH. Cayley calculó que debía haber ocho isómeros del pentanol, de fórmula C5H11OH. Todos fueron identificados posteriormente (1-pentanol, 3-metil-1-butanol, 2-metil-1-butanol, 2,2-dimetil-1-propanol, 3-pentanol, 2-pentanol, 3-metil-2-butanol y 2-metil-2-butanol), confirmando el método de Cayley.

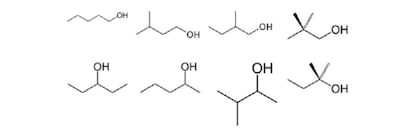
Por supuesto, existen otras maneras de clasificar los isómeros químicos (ópticos, estables, etc.). Pero The Online Encyclopedia of Integer Sequences ha seguido la teoría de Cayley para conocer el número de isómeros de alcano. Se estima que el alcano C167H336 posee más isómeros que partículas tiene el universo.

Marta Macho-Stadler es profesora del Departamento de Matemáticas de la Universidad del País Vasco y miembro de la Comisión de Género del ICMAT.

Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: "Un matemático es una máquina que transforma café en teoremas".

Edición y coordinación:Ágata Timón (ICMAT).

Puedes seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aquí a nuestra Newsletter.