Hemos descrito un nuevo objeto geométrico y lo llevas puesto

Siendo matemática casi desde chica, como se dice en mi pueblo, he tenido que escuchar (y responder) una cantidad nada despreciable de veces preguntas como ¿todavía queda algo por descubrir en matemáticas? ¿Las matemáticas se crean o se descubren?

No es mi intención en este artículo responder a la segunda pregunta en general ,porque se trata de un debate filosófico demasiado profundo para estas alturas del verano y, honestamente, si me he sentado esta tarde calurosa a escribir esta nota de divulgación es porque quiero tratar de explicarles (ojalá lo consiga) el contenido geométrico del artículo que salió publicado el pasado viernes en Nature Communications y del que soy una de las autoras. Pero, en pocas palabras, a las segunda pregunta pregunta suelo responder con “un poco de cada cosa”. Hay matemáticas que se crearon como parte de un proceso deductivo lógico y que luego fueron aplicadas con éxito a explicar la naturaleza, como las geometrías no euclídeas, y matemáticas que se descubren mirándole a los ojos a nuestro universo.

Hoy quiero explicarles un poco de estas últimas. Quiero presentarles un objeto geométrico, no descrito hasta ahora, que hemos descubierto mirando no a los ojos sino a las glándulas salivales de la mosca de la fruta. Con esto de paso respondemos también a la primera pregunta: sí, quedan muchísimas cosas que descubrir en matemáticas porque cada vez que encontramos la respuesta a un problema, en general, aparece un ramillete maravilloso de nuevas preguntas.

Quedan muchísimas cosas que descubrir en matemáticas porque cada vez que encontramos la respuesta a un problema, en general, aparece un ramillete maravilloso de nuevas preguntas

Vamos, entonces, con la mosca de la fruta. Toda esta historia comienza cuando Luisma Escudero, del Departamento de Biología Celular de la Universidad de Sevilla, contacta con Alberto Márquez y conmigo misma para pedirnos colaboración en un trabajo de morfogénesis que está llevando a cabo con su grupo de investigación. Por cierto, morfogénesis es el proceso biológico que permite que un organismo vivo desarrolle su forma. Ellos querían describir cómo se empaquetaban las células epiteliales, que son células tridimensionales, y que son, cito textualmente a Luisma, “los bloques de construcción con los que se forma un organismo.

Son como "piezas de Tente o Lego de los que están hechos los animales”. No es que su grupo hubiera tenido la feliz idea de plantearse por primera vez esa cuestión sino que, hasta la fecha, se aceptaba que los epitelios se construían empaquetando prismas o pirámides truncadas, como se muestran en la figura de la izquierda.

Pero a nuestros colegas biólogos, tras examinar las muestras de células epiteliales de la glándulas salivales de la mosca de la fruta no les convencía esta hipótesis mundialmente aceptada. Bueno, al menos en los foros de biología celular, no sabemos de su aceptación en Forocoches, por ejemplo.

Y tenían razón. Por eso hemos publicado en Nature Communications, claro. Había entonces que decidir qué figura geométrica tridimensional es la que adoptaban las células epiteliales para dar forma a los órganos. Y aquí entra en juego una estructura matemática tan intuitiva como bella y elegante que son los diagramas de Voronoi.

Así que antes de seguir con los epitelios de las moscas permítanme que les explique qué es un diagrama de Voronoi. No se asusten, es un concepto tan intuitivo, como ya he dicho, que lo puede entender hasta un niño de 3 años. O así al menos lo pensé yo el día que me tocó ir a la clase de mi hijo cuando tenía esa edad a explicar en qué trabajaba. Piensen que tienen en un plano, en una hoja de papel, por ejemplo, un conjunto de puntos dibujados (estos puntos podrían ser, por ejemplo, las farmacias de su ciudad señaladas sobre un plano).

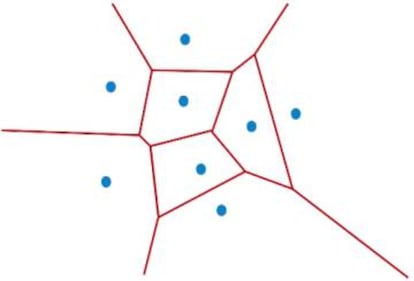
Pues bien, el diagrama de Voronoi de ese conjunto de puntos (de las farmacias) es una división del papel (del plano) en regiones de manera que a cada punto le asigna la región del papel cuyos puntos están más cerca de él que de ningún otro. Dicho para el ejemplo de las farmacias, el diagrama de Voronoi de las farmacias de la ciudad dividiría el plano de la misma en regiones de influencia de dichos establecimientos, de tal forma que a cada farmacia le asignaría la zona de la ciudad para la que ella es la más cercana. Más o menos, esta es la pinta que tiene un diagrama de Voronoi (zquierda).

A los niños del cole de Salvador se lo expliqué con los Lunnis y caramelos. Se iban a lanzar caramelos en el patio del colegio de los Lunnis y cada uno de ellos solo podrían coger los que estuviesen más cerca de él que de ningún otro y para ello, antes de lanzar caramelos, pintábamos en el suelo el diagrama de Voronoi de los Lunnis, para que no hubiese broncas (izquierda).

Como el concepto que da forma a los diagramas de Voronoi es la cercanía, la menor distancia, o la zona de influencia de los puntos, es muy fácil encontrar estos diagramas en la naturaleza. En una jirafa, por ejemplo.

Ya sabemos qué es un diagrama de Voronoi, matemáticamente hablando: la división en zonas de influencia en presencia de unos puntos generadores (ya sean farmacias o Lunnis). Con esta idea en la cabeza podemos intuir que, dado un conjunto de puntos en el plano, si hacemos crecer unos círculos al mismo ritmo tomando dichos puntos fijos como centro de dichos círculos, también se obtiene el diagrama de Voronoi. Esto queda ilustrado en la siguiente figura en la que se representan los círculos creciendo como conos con la misma apertura y vértices en los puntos a los que queremos calcular el diagrama de Voronoi (izquierda).

Ahora miramos la figura desde arriba y fíjense qué cosa tan bonita: hemos construido el diagrama de Voronoi (véase imagen que ilustra este artículo).

Volvemos a las células pero no a las epiteliales todavía, sino a células planas, en 2D. Es lógico pensar que así se empaquetan o se agrupan las células en los tejidos planos. Porque todas crecen con ‘la misma fuerza’ desde el centro de masa de la misma. Y así es. De hecho, esta idea ya fue aprovechada por el propio Luisma Escudero y algunos colaboradores para desarrollar un modelo del empaquetamiento de las células en 2D que puede servir para revolucionar el diagnóstico automatizado de ciertas formaciones tumorales.

Por si no se quieren leer el artículo les resumo a grandes trazos. Lo que hacen el Luisma y sus colegas es crear un modelo de tejido epitelial plano (y muscular) ideal mediante el siguiente procedimiento computacional:(1) se genera un conjunto de puntos al azar;(2) a dichos puntos se les calcula su diagrama de Voronoi;(3) se calcula el centro de masas de cada una de las regiones resultantes (esto nos proporciona un nuevo conjunto de puntos);(4) se calcula el diagrama de Voronoi del nuevo conjunto.

Repiten el proceso hasta tres veces más. El aspecto que tiene este quinto diagrama de Voronoi calculado es el modelo de tejido ideal (puesto que todas las células son similares, al expandirse, sus fronteras tienden a formar un diagrama de Voronoi). A partir de aquí los investigadores miden cómo de parecido es el tejido de una muestra real del tejido modelo. Si se parecen según ciertos parámetros (geométricos y topológicos), el tejido real está sano; en otro caso se concluye que algunas células no presentan las mismas características físicas que sus vecinas, lo que puede indicar el comienzo de un proceso tumoral. Ya lo sé, es algo tan sorprendente como maravilloso.

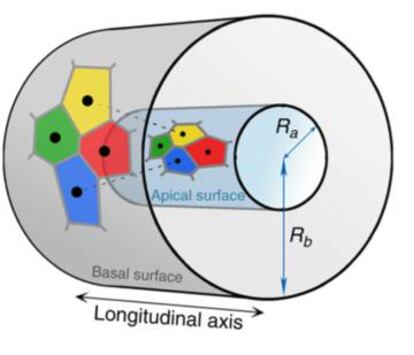
Todo esto era para células o tejidos en 2 dimensiones pero ¿qué pasa? Que las celulas epiteliales, como hemos dicho, son células tridimensionales. Pues bien, dar el paso a estructuras tridimensionales no es, ni mucho menos, trivial (que es una de las palabras favoritas de los matemáticos, sobre todo en clase de problemas). Si se trata de generalizar lo anterior obtendríamos un diagrama de Voronoi 3D que es una estructura bien bonita también pero que no se parece en nada a la organización que vemos en los tejidos epiteliales. Estos, los tejidos epiteliales, son como una capa gordita delimitada por dos superficies paralelas (denominadas superficies basal y apical) y de tal forma las mismas células que aparecen en la basal se ven la apical. Podemos pensar, solo para hacernos una idea, en que el epitelio es una rebanada gordita de pan de molde, como las de las torrijas, a la cara de arriba la llamamos cara apical y a la de abajo cara basal. No sirve para todos los epitelios porque en algunos la rebanada se enrolla en forma de cilindro hueco pero creo que puede ayudar a entender la idea. Pues bien, cada célula que vemos ‘dibujada’ en la cara apical aparecerá también en la basal.

Ello había llevado, hasta el momento, a representar las células de tejidos epiteliales como prismas con una base en la superficie basal y otra en la apical. Como si las células fuesen muchas cajitas apiñadas que formaban la rebanada y las células que se veían en las capas exteriores fuesen las tapas de esas cajitas alargadas.

Pero no, para fortuna de los autores del artículo de Nature Communications, ese modelo no se corresponde a la organización de las células en los tejidos epiteliales cuando lo miramos al microscopio. Se puede comprobar que hay células (que nos parecerán celdas de Voronoi al mirarlas) que son vecinas, por ejemplo en la capa apical, las de la cara de arriba, que dejan de serlo en la capa basal, la de abajo. Si las células fuesen prismas o pirámides truncadas esto es imposible. Tenemos que pensar que el polígono (la celda de Voronoi) que vemos en la parte de arriba de la rebanada y el que vemos abajo deberían ser las ‘tapas’ del prisma. Pero si han cambiado su posición relativa de una capa a otra es porque el prisma se ha retorcido por el camino. Y ahí está el problema. Desde el punto de vista geométrico los prismas (o pirámides truncadas) no modelan bien el problema; desde el punto de vista de la biología celular, necesitamos saber qué células están en contacto en cada punto. En la figura siguiente, correspondiente a un epitelio cilíndrico, observamos que las células amarilla y azul son vecinas en la capa apical pero han dejado de serlo en la capa basal, alguien se interpuso entre ellas (a la izquierda).

Se hace necesaria, por lo tanto, una forma geométrica que modele bien las células de los tejidos epiteliales, que se pueda plegar y adoptar distintas curvaturas, cuya forma corresponda a un modelo de equilibrio de fuerzas y que vaya desde la superficie basal hasta la apical, pero sin tener que tener los mismos contactos en ambas superficies.La solución a todo ello es el escutoide. Déjenme que ponga aquí mi figura favorita del artículo; los escutoides hechos con plastilina de Luisma Escudero (izquierda).

Monísimos, ¿verdad? Por cierto, le llamamos escutoides porque fue él, Luisma Escudero, el primero en clamar que aquello no eran prismas y en hacerlos con la plastilina de Margarita (su hija): Escu-dero-escu-toide. Cuando vimos que salía algo muy publicable buscamos una justificación más formal que esta y, bueno, se parece al scutum del tórax de los escarabajos de la especie Protaetia speciosa.

Curiosamente, desde que salió el artículo el viernes pasado, en Twitter alguien dijo que scutoid (el nombre en inglés) es ideal porque es una figura geométrica muy cute. A mí también me lo parece. Aquí les dejo uno de los dibujos que los internautas han publicado (a la izquierda, por @atheblerr).

Seguimos. El escutoide, técnicamente, se obtiene a partir de segmentos perpendiculares a todas las capas comprendidas entre la capa apical (la de arriba) y la capa basal (la de abajo). Para ello, se eligen un conjunto de puntos (semillas) en la capa apical, por ejemplo. Se trazan los segmentos perpendiculares a la capa apical en cada uno de estas semillas. En cada capa comprendida entre la apical y la basal, cada segmento producirá una intersección (una nueva semilla); a estas semillas nuevas les calculamos diagramas de Voronoi en dicha capa (de forma similar a como se hace en el plano, pero hay que adaptar algo las técnicas). Ahora ‘pegando’ las regiones de Voronoi (que serán polígonos) correspondientes a todos los puntos de un mismo segmento se obtiene un escutoide.

Si lo que buscamos es una descripción más simple podemos decir que un escutoide es un sólido geométrico entre dos capas paralelas (la basal y la apical) de tal forma que la intersección del escutoide en cada una de las dos capas (y en el resto de las capas intermedias también) son polígonos (lo que serían las ‘tapas’ del escutoide). Los vértices de estos dos polígonos están unidos por una curva o por una conexión en forma de Y. Las caras de los escutoides no son necesariamente convexas, pueden tener huecos hacía dentro, por lo que varios escutoides pueden empaquetarse para llenar todo el espacio entre las dos superficies paralelas. Y sí, parecen un juego de salpimentero de diseño.

¿Y todo esto para qué? ¿Por qué se complica tanto la Naturaleza? La respuesta a estas preguntas viene de la mano del físico del equipo, Javier Buceta, del Departamento de Bioingeniería de la Universidad de Lehigh. Según el análisis de Javier, la forma del escutoide es consistente con las fuerzas involucradas y se alcanza con ella una posición de equilibrio. Dicho de otra forma, esta estructura, el escutoide, es más favorable para el tejido desde el punto de vista energético y esto es importante porque facilita adoptar formas muy diferentes, que es lo necesario para que se establezcan bien los órganos y funcionen correctamente.

Maravilloso, ¿verdad?

Esta estructura escutoidal ha sido encontrada y verificada en algunos modelos básicos de biología celular: las glándulas salivales de la mosca de la fruta, sus huevos y en células de pez cebra.

Y ahora viene lo mejor: las implicaciones del trabajo. Conocer con este nivel de detalle la estructura de las células epiteliales puede ser fundamental para la creación de órganos con impresión 3D y nos permitirá identificar modelos de epitelios sanos, a partir de su geometría, que servirán como patrones para detectar un crecimiento celular anómalo.

Está mal que lo diga yo que soy una de las autoras pero el trabajo me parece tan bello como interesante, una mezcla maravillosa y elegante de disciplinas (biología celular, física y matemáticas) y quién sabe, si una puerta abierta a nuevos avance en biomedicina.

Los nombres de todos los autores y su filiación se pueden consultar aquí pero, básicamente, el estudio ha sido liderado por Luisma Escudero, del Departamento de Biología Celular de la Universidad de Sevilla e Instituto de Biomedicina de Sevilla y su grupo de investigación; el análisis físico ha estado en las manos de Javier Buceta de la Universidad de Lehigh y Alberto Márquez y la que firma, también de la Universidad de Sevilla, hemos colaborado en la parte del modelo matemático.

Disfruten del verano, ustedes y los escutoides que llevan puestos en sus epitelios.