Un cuadrado triangulado de una forma muy especial

Hoy vamos a hablar sobre triangulaciones de un cuadrado, es decir, de dividir un cuadrado en triángulos. En este blog ya hemos hablado sobre triangulaciones de polígonos, concretamente en Tetraedrizando, que es gerundio, pero en este caso vamos a profundizar un poco más estudiando unas muy concretas.

Lo que queremos es triangular un cuadrado de forma que todos los triángulos que nos queden tengan exactamente la misma área. En aquel momento, no nos preocupamos por el área de los triángulos, pero ahora queremos que todas las áreas sean exactamente iguales.

Imaginemos que queremos dividir un cuadrado en n triángulos con la misma área. Hay una forma sencilla de hacer esto:

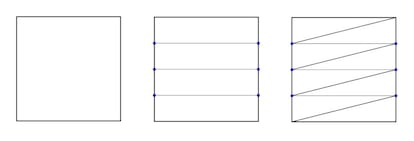
- Dividimos dos lados opuestos del cuadrado, por ejemplo los verticales, en n/2 segmentos de la misma longitud.

- Unimos los puntos que queden a la misma altura con segmentos. Nos queda n/2 rectángulos iguales.

- Dividimos cada rectángulo en dos triángulos trazando una de las diagonales. Obtenemos así n/2 triángulos de la misma área.

En la siguiente imagen podéis ver un ejemplo en el que hemos dividido el cuadrado inicial en 8 triángulos de la misma área:

Problema resuelto, ¿verdad? Pues sí y no. Con este procedimiento podemos hacer la triangulación que queríamos, pero si os fijáis obtendremos siempre un número par de triángulos. La pregunta realmente interesante en este asunto es la siguiente: ¿podemos triangular un cuadrado de manera que nos quede un número impar de triángulos de la misma área? Podéis pensar en ello antes de seguir leyendo, por ejemplo buscando una triangulación con tres triángulos (el caso más simple en teoría), a ver si se os ocurre alguna manera de hacerlo.

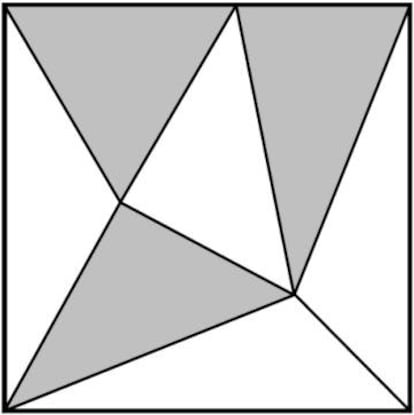
Tened en cuenta una cosa: los triángulos tienen que tener la misma área, pero no hace falta que sean exactamente iguales en forma. En la imagen podéis ver una posible triangulación impar…que, por desgracia, es incorrecta, ya que en realidad no todos los triángulos tienen la misma área (por poco).

Adentrémonos un poco más en el tema. Sorprendentemente, la primera referencia de alguien que se preguntó si un cuadrado poseía una triangulación impar fue Fred Richman en 1965. Y decimos sorprendentemente porque esta cuestión tiene pinta de problema que podría haberse estudiado en la Grecia clásica. El caso es que, a partir de esto, un compañero de Richman, John Thomas, consiguió demostrar que no existen triangulaciones impares si las coordenadas de los vértices de los triángulos tenían ciertas características (más concretamente, si eran todas racionales con denominador impar).

Thomas envió su trabajo a una publicación, y el revisor le dijo que tenía pinta de ser una cuestión sencilla y muy estudiada, por lo que le propuso que lo mandara en forma de problema para los lectores y que, si en un tiempo no lo habían resuelto, se lo publicarían. Y eso teniendo en cuenta que dicho revisor no consiguió demostrar por sí mismo el resultado de Thomas y tampoco consiguió encontrar ninguna referencia anterior al mismo. ¿Qué acabó ocurriendo? Que se publicó unos años después, en 1968.

Pero esto no resolvía el problema, seguíamos sin saber si existen triangulaciones impares de un cuadrado en el caso general…hasta 1970. En ese año, Paul Monsky demostraba el caso general a partir del trabajo del propio Thomas. Os presento el teorema de Monsky:

No es posible dividir un cuadrado en un número impar de triángulos de la misma área.

Para demostrar esto, Monsky utilizó de manera muy inteligente ciertas herramientas algebraicas (sí, algebraicas) y un bonito resultado conocido como lema de Sperner, que podemos enunciar de la siguiente forma:

Toma un triángulo cualquiera y numera los vértices con los números 1, 2 y 3. Ahora divide el triángulo en triangulitos más pequeños, los que quieras y como quieras, pero cuidándote de que dos lados de los triángulos interiores o no se toquen o se toquen en un vértice. Los nuevos vértices que hayan aparecido entre el 1 y el 2 del inicial numéralos con unos o doses a tu gusto; los que hayan aparecido entre el 1 y el 3 del inicial numéralos con unos o treses, también como prefieras; y lo mismo con los que haya entre el 2 y el 3 del inicial, ponle doses o treses como te apetezca. A los vértices que hayan surgido dentro del triángulo ponle unos, doses o treses a tu antojo.

Entonces, seguro que habrá al menos un triangulito pequeño cuyos vértices estén numerados como el inicial, con un 1, un 2 y un 3. De hecho, el número de triangulitos que cumple esto es impar.

Os invito a que hagáis vosotros el dibujo del triángulo, la división en triangulitos y la numeración de vértices para que lo veáis con vuestros propios ojos.

Los interesados en ver la demostración completa del teorema pueden consultar el propio trabajo de Monsky, On Dividing a Square into triangles. Y quienes quieran ampliar información sobre este tema también pueden leer Cutting a Polygon into Triangles of Equal Areas, de Sherman Stein, y One square and an odd number of triangles, de M. Aigner y G. M. Ziegler. En ellos, además de la demostración de Monsky, podréis ver generalizaciones del problema a otros polígonos y también a tres dimensiones.

Y para terminar, un detalle: hasta donde yo sé, no se conoce ninguna otra demostración de la no existencia de triangulaciones impares de un cuadrado aparte de la de Monsky. Si alguien tiene más información al respecto, estaremos encantados de que nos hable sobre ello en los comentarios.