Tetraedrizando, que es gerundio

Se sabe desde hace mucho tiempo que todo polígono es triangulable. La triangulación de polígonos es un proceso muy útil en diversas situaciones, y el hecho de que todo polígono se pueda triangular facilita mucho las cosas a la hora de, por ejemplo, calcular áreas de figuras irregulares.

Lo anterior significa que todo polígono, figura bidimensional limitada por segmentos, puede descomponerse en figuras cuya forma es el polígono con el menor número de lados posibles: el triángulo. Pero, posiblemente, lo que muchos no os habéis preguntado es si se puede hacer lo mismo en tres dimensiones, es decir, si cualquier poliedro (figura tridimensional limitada por polígonos, llamadas caras) puede descomponerse en distintas partes cuya forma sea el poliedro con el menor número de caras posible: el tetraedro. La pregunta sería algo así: ¿todo poliedro es tetraedrizable?

Antes de nada, vamos a comentar qué es exactamente triangular un polígono. Una triangulación de un polígono es una división de dicho polígono en triángulos que cumple que la unión de todos los triángulos da el polígono inicial, que todos los vértices de los triángulos son vértices del polígono inicial (es decir, no añadimos ni quitamos vértices) y que todos los triángulos comparten entre sí, como mucho, un vértice o un lado.

Con estas condiciones, todo polígono es triangulable. Por ver un ejemplo, os dejo aquí una triangulación de un polígono de once lados:

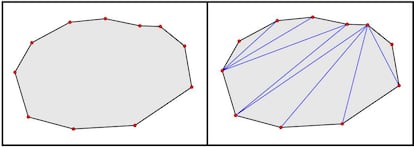
Como hemos comentado, triangular un polígono puede ser muy interesante para, por ejemplo, calcular áreas de figuras poligonales extrañas. La idea sería triangular esa superficie bidimensional y aprovechar que el área de un triángulo es muy fácil de calcular (base por altura dividido entre 2). Calculamos las áreas de todos los triángulos, sumamos y ya tenemos el área de la figura inicial.

Visto esto, la cuestión ahora es preguntarse qué ocurre en tres dimensiones. Ya hemos visto por aquí que, en ocasiones, el paso a tres dimensiones es complicado, como pasaba en el problema de los besos de las esferas. Veamos qué ocurre en este caso.

Como decíamos antes, la idea es ver si puede dividirse cualquier poliedro en tetraedros, que es el poliedro con el menor número posible de caras. Vamos, nos preguntamos lo siguiente: ¿todo poliedro es tetraedrizable? Se entiende, con unas condiciones equivalentes al caso de la triangulación: que la unión de los tetraedros sea el poliedro inicial, que todos los vértices de los tetraedros sean vértices del inicial (es decir, que no haya que añadir ni quitar vértices) y que cada dos tetraedros compartan, como mucho, un vértice, una arista o una cara.

En lo que se refiere a triangular un polígono, se puede hacer tanto si el polígono es convexo como si no lo es. Con los poliedros no ocurre eso: todo poliedro convexo es tetraedrizable, pero no todo poliedro no convexo es tetraedrizable. Este descubrimiento es relativamente reciente, concretamente de 1911. En ese año, N. J. Lennes construyó un poliedro no convexo que no era tetraedrizable. Algo después, en 1928, Eric Schönhardt dio un ejemplo más sencillo simplificando la construcción anterior, quedando el que ahora se conoce como poliedro de Schönhardt:

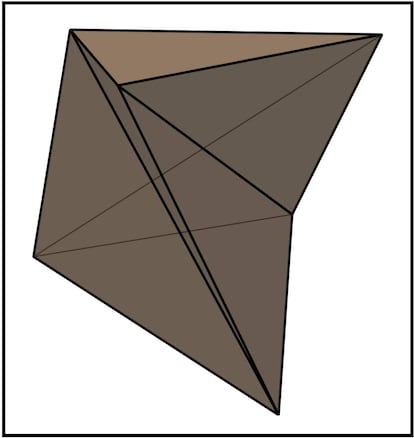
Extraño, ¿verdad? Es posible que con esa imagen uno no sea capaz de construirse una buena idea mental de esta figura. Por ello, os dejo este vídeo en el que se ve en movimiento a este curioso poliedro:

Para finalizar, es interesante comentar que éste no es el único caso de poliedro no tetraedrizable. Después del de Schönhardt, se descubrieron más figuras poliédricas que no pueden dividirse en tetraedros con las condiciones descritas. Algunos ejemplos son el poliedro de Thurston y el poliedro de Chazelle. En The Geometry Junkyard tenéis más información sobre ellos.

En matemáticas, el hecho de que al pasar de dos a tres dimensiones cambien características o se pierdan propiedades es, posiblemente, más habitual de lo que uno podría esperar. Hay muchos más ejemplos de situaciones en las que ocurren cosas parecidas a la que ocurre con las tetraedrizaciones. Seguro que vosotros conocéis más casos, y si es así estaremos muy agradecidos si los compartís con nosotros en los comentarios.