El curioso caso de la secuencia de Goodstein
Un llamativo caso en el que las matemáticas vuelven a atentar contra nuestra intuición
Hacer caso de nuestra propia intuición puede ser interesante en algunas ocasiones, pero en otras puede hacer que nos precipitemos y escojamos la opción equivocada (recordad, por poner un ejemplo, la paradoja de la banda esférica). Y en matemáticas eso pasa mucho: es peligroso fiarse de nuestra intuición cuando estamos tratando con resultados matemáticos.
Hoy vamos a ver un caso bastante curioso en el que este peligro hace acto de presencia: vamos a adentrarnos en el curioso caso de la secuencia de Goodstein.
Dejémonos de preámbulos y metámonos ya en el tema. Para cada entero positivo vamos a definir una secuencia de números y después intentaremos analizar cómo podría terminar dicha secuencia. Para mostrar esta secuencia de números, vamos a verlo con un ejemplo.
Tomamos el número 124 y lo expresamos como suma de potencias de 2 (todo entero positivo puede expresarse de esa forma):
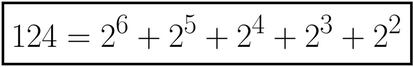
Ahora, expresamos todos los exponentes también como potencias de 2 (los que sean 2 o menores se dejan igual):
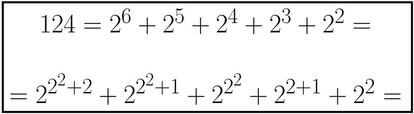
Hecho esto, sustituimos todas las apariciones del número 2 por un número 3 y restamos 1 al resultado, quedándonos la siguiente expresión:
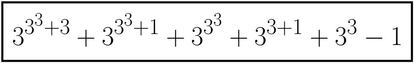
que, más concretamente, es el número 236393522034704. La cosa ha crecido bastante, ¿verdad? Bien, expresemos ahora este número en forma de suma en base 3, para lo cual haremos uso de la igualdad
(an – 1) = (a – 1) · (an-1 + an-2 + … + a + 1)
para “quitar” esa resta final:
Calculemos un valor más de la sucesión cambiando el 3 por el 4 y restando de nuevo 1 al resultado:
Nos queda un número de 157 cifras, muchísimo mayor que los anteriores. Y ahora haríamos lo mismo cambiando el 4 por el 5 y restando 1; y después cambiando el 5 por el 6 y restando 1; y así sucesivamente. Cada uno de los números obtenidos es un término de la sucesión de Goodstein de 124. La pregunta es: ¿cuál será el comportamiento de la sucesión? ¿Es siempre creciente? ¿Decrece en algún momento? ¿Se estabiliza alrededor de algún valor?
Está más o menos claro, ¿verdad? En cada paso, cambiamos las apariciones de un cierto número por otro una unidad mayor, con lo que las potencias son cada vez mucho más grandes, y luego solamente restamos 1, con lo que el número apenas cambia.
Teniendo en cuenta esto, está claro que la sucesión seguirá creciendo indefinidamente, ¿verdad? Pues no. La cosa es que, sorprendentemente, la sucesión de Goodstein de todo (repito, de TODO) entero positivo termina en 0 en un número finito de pasos.
Toda secuencia de Goodstein termina irremediablemente en cero.
Sí, estoy totalmente en serio: comencemos con el número que comencemos, al realizar las operaciones descritas para construir la sucesión de Goodstein, acabaremos obteniendo 0 en un número finito de pasos. No me digáis que no es para quedarse con la boca abierta.
Este resultado fue demostrado por primera vez por el matemático inglés Reuben Goodstein en 1944 en su trabajo On the Restricted Ordinal Theorem.
¡ALERTA DE CONTENIDO MATEMÁTICO AVANZADO!
Este teorema de Goodstein fue uno de los primeros resultados para los cuales se demostró que no podían ser probados dentro de la aritmética de Peano (ahora no se me ocurre cómo se puede demostrar algo así). Para probarlo, Goodstein utilizó la teoría de ordinales, y más adelante se han desarrollado demostraciones que utilizan sistemas lógicos más fuertes que la aritmética de Peano.
¡FIN DE LA ALERTA!
Intentar comprobar el resultado con algún número pequeño puede darnos una idea de por qué ocurre esto tan contrario a nuestra intuición. Veamos qué pasa si comenzamos con el número 3:
Como veis, la sucesión termina en 0, como dice el teorema de Goodstein.
Podéis comenzar ahora en el número 4 para ver otro ejemplo, pero os aviso de que en ese caso tendréis que realizar una cantidad inimaginable de pasos hasta llegar a 0 (se alcanza un número de más de 121 millones de cifras). Pero se llega, os aseguro que se llega.
Como curiosidad final, es interesante comentar que este teorema se puede generalizar a un cambio de base cualquiera en cada paso. Es decir, no hace falta cambiar por el número siguiente (el 2 por el 3, el 3 por el 4, etcétera), sino que podríamos cambiar por cualquier entero positivo en cada paso y el teorema se seguiría cumpliendo. Sencillamente maravilloso.
Y ahora os toca a vosotros. Me gustaría, si os apetece, que nos hablarais en los comentarios de resultados matemáticos contrarios a la intuición pero que sean ciertos. Hay muchos, así que seguro que podemos coleccionar unos cuantos y, por qué no, hablar de algunos de ellos en próximos artículos.
