Una paradoja de pelotas

Según el Diccionario de la RAE, el término “paradoja”, en su segunda acepción, se define de la siguiente forma:

Paradoja: Hecho o expresión aparentemente contrarios a la lógica.

A nuestro alrededor, en nuestra vida diaria, podemos encontrar muchas cuestiones que podrían encuadrarse dentro del mundo de las paradojas, pero dejemos éstas aparte y centrémonos en el tema del que trata este blog: las matemáticas.

En matemáticas no es difícil encontrarse con paradojas de todo tipo (como, por ejemplo, la paradoja de Bertrand de la que hablamos hace un tiempo): las hay relacionadas con la lógica en sí misma, con la teoría de conjuntos, con la probabilidad, con el cálculo, con la geometría…

Relacionada con esta última rama de las matemáticas está la paradoja que vamos a analizar en este artículo. Su nombre, paradoja de la banda esférica, quizás no nos muestre demasiado sobre su contenido, pero sí que más o menos nos induce a pensar que la cosa va “de pelotas”. Veamos de qué trata el asunto.

Supongamos que tenemos una esfera pequeña, digamos del tamaño de una pelota de ping pong. Tomamos un hilo y la rodeamos completamente por su ecuador, nos quedamos con el trocito que hemos usado para rodear y le añadimos un metro más de hilo. Después, colocamos el hilo obtenido (el que salió al rodear junto con el metro añadido) alrededor del ecuador. Como quedará espacio entre nuestro hilo y el ecuador, intentamos que dicho espacio sea el mismo para todos los puntos (es decir, que el hilo y el ecuador estén a la misma distancia en todos los puntos). Hecho esto, nos preguntamos lo siguiente: ¿el hueco que queda entre hilo y pelota es muy grande o muy pequeño? ¿Podríamos pasar a través de él un bolígrafo BIC con capucha (de, en total, unos 15 cm de altura)?

Tomemos ahora una esfera mayor, por ejemplo una del tamaño del típico mapamundi que muchos hemos tenido en casa en algún momento, y hagamos lo mismo: hilo alrededor del ecuador, añadimos un metro de hilo al trozo obtenido al rodear y colocamos el hilo resultante alrededor del ecuador dejando, en todos los puntos, el mismo espacio. ¿Cómo será ahora el hueco que hemos obtenido? ¿Podremos ahora hacer pasar el bolígrafo por él?

Y ahora a lo grande, por qué no: tomemos una esfera del tamaño de nuestro planeta y repitamos la operación: rodeamos el ecuador con un hilo, después lo aumentamos un metro y a continuación lo colocamos a distancia uniforme del ecuador. ¿Qué tamaño tendrá este hueco en relación con los anteriores? ¿Pasará ahora nuestro boli por dicho hueco?

Como podéis ver, los tamaños de las esferas elegidas son distintos, bastante distintos (de una pelota de ping pong a una esfera como La Tierra va un buen trecho…). Lo más habitual, al menos lo que más ha ocurrido cuando he planteado esta cuestión a alguien, es que nuestra intuición nos diga que el boli pasará fácilmente por el hueco que queda con la pelota de ping pong, que le cueste más con el que deja el mapamundi (o que incluso no pase) y que ni de broma quepa por el hueco obtenido con una esfera como nuestro planeta.

Bien, pues la solución es la siguiente: los tres huecos son exactamente iguales. En cada punto del ecuador de las tres esferas, la distancia entre dicho punto y el que le correspondería en el hilo alargado es exactamente la misma. ¿Os ha chocado el resultado? ¿Queréis ver cómo calcular dicha distancia con unas matemáticas muy simples? Seguid leyendo.

En general, lo que ocurre es que el hueco que queda entre hilo y ecuador es independiente del radio de la esfera inicial, por lo que tomemos la esfera que tomemos obtendremos que el hueco tiene siempre el mismo tamaño. Vamos a tomar una esfera de radio R cualquiera, medido en metros, y hagamos cálculos.

Calculamos la longitud del ecuador con la fórmula para calcular la longitud de una circunferencia:

L = 2 · π · R

Ésa sería la longitud del hilo con el que rodeamos la esfera. Ahora añadimos un metro a ese hilo, obteniendo la longitud de la circunferencia que quedaría separada de nuestra esfera:

L’ = 2 · π · R + 1

Pero esta longitud se puede calcular de otra manera. Pensad que la nueva circunferencia tendrá como radio el de la inicial, R, más un poco más, digamos r, que de hecho es la distancia que queremos calcular. Como el radio de la misma será entonces R + r, su longitud puede calcularse así:

L’ = 2 · π · (R + r)

Vamos a calcular la distancia que buscamos, r, igualando las dos expresiones de L’ y despejando:

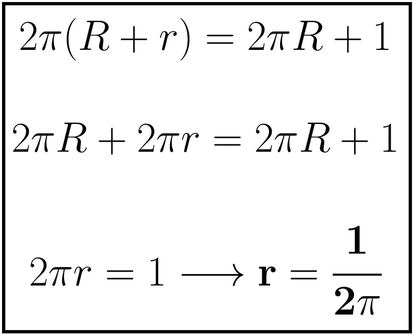
Hemos obtenido que r (la distancia buscada) es, efectivamente, independiente del radio de la esfera inicial y, además, que su valor es 1 dividido entre 2π. Ese valor es 0’159154…, con lo que, teniendo en cuenta que hemos considerado que r viene expresado en metros, tenemos que la distancia en cada punto entre hilo y ecuador es de casi 16 cm. Por tanto, en los tres ejemplos mostrados más arriba (y con cualquier otra esfera, sea del tamaño que sea), nuestro boli BIC pasará sin demasiada dificultad por el hueco obtenido.

¿Os ha sorprendido el resultado? Si pensasteis que los huecos eran de tamaños distintos no os preocupéis. Tiene cierto sentido pensar eso, ya que si relacionamos el hueco con el tamaño de la esfera, tenemos que cuando más pequeña es dicha esfera más grande se vería ese hueco en relación con ella. Pero, como habéis visto, las matemáticas nos aseguran que da igual si tomamos inicialmente una canica, un balón de baloncesto o una esfera un millón de veces mayor que nuestro Sol, en todos los casos el hueco sería el mismo: 16 cm. Curioso, ¿verdad?

¿Habéis pensado que los huecos iban siendo cada vez más pequeños? ¿O vuestra intuición os dijo otra cosa? Contadnos en los comentarios qué os ha sugerido el problema, seguro que es interesante ver lo que ha pensado cada uno de vosotros. Y, ya de paso, si nos habláis de alguna otra paradoja que sea digna de comentar por aquí mucho mejor.