¿Existen poliedros “agujereados” que no tengan diagonales?

En el mundo de las matemáticas podemos encontrar muchos submundos que, aunque sea parcelas muy concretas y acotadas, esconden una gran cantidad de curiosidades dignas de ser estudiadas y analizadas. Uno de esos submundos, que será el protagonista de este artículo, es el de los poliedros.

Como ya sabemos, podemos definir poliedro como una figura tridimensional limitada por polígonos que encierra un volumen finito. Hay muchos poliedros que tienen características destacables, como los regulares, los semirregulares, los arquimedianos, etc. Esta definición puede generalizarse a cualquier dimensión, y el nombre general pasaría a ser polítopo. Como curiosidad, comentar que en dimensión cero hay un solo polítopo regular, al igual que en dimensión uno; en dimensión dos hay infinitos polítopos regulares (todos los polígonos regulares); en dimensión tres tenemos cinco (los cinco poliedros regulares); en dimensión cuatro tenemos seis; y de dimensión cinco en adelante hay exactamente tres polítopos regulares.

Volvamos a los poliedros, a los tridimensionales. De ellos ya hablamos aquí en el artículo dedicado a la fórmula de Euler, y también cuando analizamos qué poliedros se podían tetraedrizar o cuando contamos la historia de Matt Parker y el balón imposible. Hoy vamos a hablar de un poliedro muy concreto que tiene unas características y unas propiedades bastante interesantes: el poliedro de Császár.

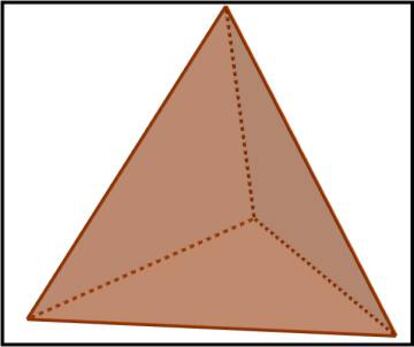
Comencemos hablando del tetraedro. Si os fijáis, el tetraedro no tiene diagonales, cada pareja de vértices está ya unido por una arista, por lo que no hay ninguna pareja de aristas “libres” para que sean unidas por un nuevo segmento, que es al que llamaríamos “diagonal”. Por otra parte, si imaginamos el tetraedro como una figura de plastilina, podríamos deformarlo (sin romperlo) hasta convertirlo en una esfera. Bien, pues el tetraedro es el único poliedro deformable en una esfera que cumple que no tiene diagonales.

En 1949, el matemático húngaro Ákos Császár se preguntó sobre si habría algún poliedro no deformable en una esfera (esto es, que tuviera algún “agujero” que impidiera convertirlo en una esfera) que cumpliera lo mismo que el tetraedro, que no tuviera diagonales. Y lo encontró. En su trabajo A polyhedron without diagonals, Ákos responde a esta pregunta demostrando que sí existe tal poliedro, que acabó llamándose poliedro de Császár:

Como en la imagen no se aprecia bien el poliedro en toda su extensión, os dejo el siguiente vídeo (tomado de la Wikipedia) en el que podemos verlo mucho mejor y, además, ver también su desarrollo plano:

Este curioso poliedro es no convexo (tiene un agujero), y posee 7 vértices, 21 aristas y 14 caras, todas ellas triángulos. No cumple la fórmula de Euler, ya que

14 – 21 – 7 = 0 ≠ 2

y, como puede verse en el vídeo, no tiene diagonales: todas las parejas posibles de vértices están ya unidos con una arista.

Como curiosidad, y hasta donde yo sé, no se conocen poliedros (convexos o no) que no tengan diagonales salvo el tetraedro y este poliedro de Császár. Si alguien tiene información nueva a este respecto, estaremos muy agradecidos si la comparte con nosotros en los comentarios.

Creo que es bastante evidente que el poliedro de Császár tiene una forma algo extraña, por lo que se podría pensar que es complicado de construir. ¡¡Nada de eso!! De hecho no es demasiado difícil de montar…si nos dan una buena plantilla de su desarrollo plano en dos dimensiones que nos ayude a ello. Y en El Aleph estamos para eso.

Podríais reconstruir la que se ve en el vídeo, pero seguro que preferís que os la den ya hecha. Pues aquí os dejo una muy buena plantilla del poliedro de Császár junto con alguna pequeña instrucción para montarlo, gracias a la magnífica web CutOutFoldUp: plantilla del poliedro de Császár en CutOutFoldUp. Desde este blog, os animamos a que os descarguéis la plantilla e intentéis montar el poliedro, y a que, si queréis, nos dejéis una foto de vuestra obra maestra en los comentarios.

Relacionado con este poliedro tenemos otro también con una forma y unas características muy curiosas: el poliedro de Szilassi, descubierto por el matemático Lajos Szilassi en 1977. Este poliedro es el dual del poliedro de Császár. Os dejo que investiguéis sobre cómo construirlo y sobre sus propiedades.

Y, para terminar, una curiosidad relacionada con la tetraedrización de la que hablamos en este artículo. ¿Es tetraedrizable el poliedro de Császár? Pues la respuesta es sí, el poliedro de Császár se puede tetraedrizar. Podéis verlo en Wolfram Demonstrations Project.