El joven de 28 años que revolucionó los ‘rayos de luz’

Ayer, 23 de abril, se cumplió el 190 aniversario de la teoría de los sistemas de rayos, uno de los grandes tratados de la óptica propuesto por Sir W.R. Hamilton, físico y matemático irlandés, que con solo 28 años se consolidó como el renovador de la teoría de la luz establecida hasta el siglo XIX. Desde una temprana edad, Hamilton había demostrado una gran destreza para las matemáticas: dominaba el cálculo integral y la astronomía, podía predecir eclipses y había leído a Newton y a Lagrange. Aun así, Hamilton tuvo que relegar las ciencias a un segundo plano, porque para acceder a la universidad, al Trinity College en Dublín, tuvo que dedicarse el estudio de Humanidades. Antes de su ingreso en la universidad en 1823 comunicó a su primo Arthur, por carta, el preludio de sus grandes logros. Allí decía: “En óptica, he hecho un descubrimiento muy curioso, al menos así me lo parece...”

Más información

El dodecaedro maldito

La impredecibilidad humana ayuda a ‘tumbar’ una teoría de Einstein

Entre estas ideas que esbozaba a su primo, estaba la descripción geométrica de los rayos de luz: “Un rayo debe ser considerado como una línea recta o curva por la que se propaga la luz; y un sistema de rayos como una colección de tales líneas, con un origen común. Así, los rayos que divergen desde un punto luminoso componen un sistema óptico, y, después que se han reflejado en un espejo, componen otro”. Hamilton analizaba cómo se comportan los rayos en diferentes medios: si divergen o convergen, si son paralelos, la relación entre el ángulo de incidencia y el ángulo de refracción, sus combinaciones en haces, etc. Además, formalizó la dinámica de estos haces de manera global e independiente de la naturaleza del proceso óptico, de forma que su teoría podía aplicarse posteriormente a otros procesos físicos.

Con estos textos, Hamilton renovó las concepciones iniciales sobre la óptica, como las teorías algebraicas de Malus, un oficial de ingenieros del ejército de Napoleón en Egipto que descubrió la polarización de la luz y propuso un profundo tratado matemático sobre su propagación. La dificultad de sus cálculos y el uso de geometría y álgebra no trivial inspiró a Hamilton para formular un principio que resumiera toda la teoría de forma mucho más compacta y sencilla.

Su idea “abarcaba todo lo descubierto acerca de las formas y posiciones de las líneas a lo largo de las cuales se propaga la luz”, según señalaba Hamilton. Su enunciado fundamental, el ahora conocido como “principio de mínima acción”, puede resumirse en una frase: “un rayo de luz siempre recorre el camino en que el tiempo de transcurso de un punto a otro es mínimo”.

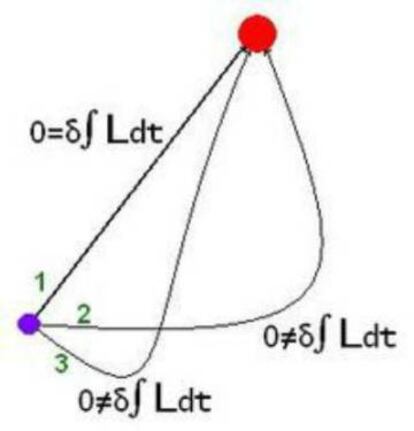
En la figura se ven posibles caminos que podría elegir un rayo de luz al propagarse en un medio entre dos puntos. El principio de mínima acción dicta, en palabras matemáticas, que el camino predilecto será la solución del llamado problema de puntos críticos de un funcional de acción, es decir, se tratará de maximizar o minimizar la integral de una función en un intervalo de tiempo cuyos extremos son fijos, denominada función Lagrangiana, que depende de las coordenadas del espacio, de las velocidades y del tiempo. Este principio dio lugar a las famosas ecuaciones de Euler-Lagrange de la mecánica clásica, que constituyeron una teoría equivalente a la mecánica de Newton, sin necesidad de añadir términos de fuerza en este formalismo.

Un siglo después, el principio de mínima acción se generalizó a la mecánica cuántica y la física atómica, consolidando la teoría como un marco común para procesos clásicos y cuánticos. No obstante, Hamilton fue un hombre que siempre concedió poca importancia a sus trabajos, frente a la opinión ajena y común de que todos sus estudios fueron verdaderas obras maestras, y hasta han sido grabadas en piedra.

Aquí, según caminaba Sir Willam Rowan Hamilton un 18 de Octubre de 1846, en un flash de ingenio, descubrió la fórmula fundamental multiplicativa de los cuaterniones:

i² = j² = k² = ijk = −1

y quedó inscrita en una piedra de este puente.

Los llamados cuaterniones, ideados por el matemático mientras paseaba con su esposa por su Irlanda natal, son una generalización de los números reales, similar a la de los números complejos pero con tres unidades imaginarias i, j, k, en vez de una. Más allá de su importancia en el álgebra, estos números tienen aplicaciones en física: representan rotaciones en el espacio, se emplean en el electromagnetismo, en la mecánica cuántica y hasta en robótica. 

Hamilton fue un hombre verdaderamente entregado a la ciencia, sin ánimo de celebración soberbia de sus triunfos. Y así lo constató finalmente: “Desde hace mucho tiempo he admirado la descripción que hace Ptolomeo de su gran maestro astronómico Hiparco, como un hombre que amó el trabajo y que amó la verdad. Será mi epitafio”.

Cristina Sardón es investigadora postdoctoral Severo Ochoa en el ICMAT.

Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales, y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.