No solo de números consecutivos vive el cuadrado mágico

En el artículo de la semana pasada hablábamos sobre cuadrados mágicos. En aquella ocasión, nos centramos en los cuadrados mágicos que contienen números consecutivos desde 1 en adelante (hasta n² si el cuadrado tiene n filas y n columnas), pero comentábamos que había muchos otros tipos. El mundo de los cuadrados mágicos es mucho más variado, y hoy vamos a ver unos cuantos ejemplos de esta variedad.

En los cuadrados mágicos numéricos, no siempre se cumple que todos los números son distintos. Es evidente que si todos los números son iguales, el cuadrado resultante es trivialmente mágico, pero repitiendo sólo algunos aparecen también cosas interesantes. Uno de los ejemplos más conocidos de este tipo de cuadrados mágicos es que aparece en la llamada Fachada de la Pasión de La Sagrada Familia de Barcelona. Es éste:

Aparte de que hay algún número repetido, y de que todas las filas, todas las columnas y las dos diagonales suman 33, en este cuadrado mágico hay muchas más combinaciones numéricas que suman esa cantidad. En la imagen podéis ver algunas de ellas, pero hay más. Os animo a que las busquéis y nos lo contéis en los comentarios.

Volvamos a los cuadrados con números distintos. ¿Qué os parece uno solamente con números primos? Los hay, y con números primos consecutivos. Aquí tenéis uno que contiene todos los números primos desde el 79 hasta el 439, cuya constante mágica (suma de filas, columnas y diagonales) es 2016:

En Magic Square with Sequential Prime Numbers podéis ver otros cuadrados mágicos de distintos tamaños que contienen números primos consecutivos.

Hasta ahora, en todos los cuadrados mágicos que os he presentado la operación que usamos es la suma. ¿Podremos encontrar cuadrados mágicos relacionados con otra operación? Pues sí, hay cuadrados mágicos de productos. Es decir, cuadrados mágicos en los que todas las filas, todas las columnas y las dos diagonales dan el mismo resultado al multiplicar sus términos. De ellos trataba uno de los desafíos matemáticos que propuso El País, en colaboración con la RSME, en el año 2011. Aquí tenéis, como ejemplo, un cuadrado mágico de productos de orden 3.

Pero los hay más grandes, claro que los hay. Aquí tenéis uno de orden 8 que cumple que todas sus filas, todas sus columnas y las dos diagonales tienen como producto el número 2058068231856000:

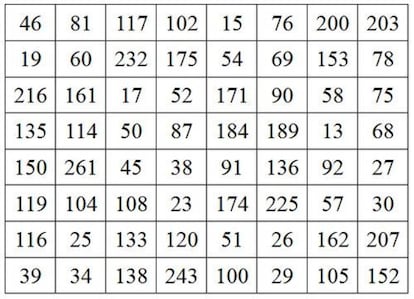
Magnífico, ¿verdad? Bien, probad ahora a sumar sus filas. Correcto, todas suman 840. ¿Y cuánto suman sus columnas? Pues sí, 840. ¿Y sus diagonales? Efectivamente, 840. Estamos ante un cuadrado numérico de orden 8 que es mágico para sumas y también para productos. Maravilloso.

Estos cuadrados que son mágicos para sumas y productos no son los únicos que rebosan magia para dos operaciones. Echad un ojo a este cuadrado:

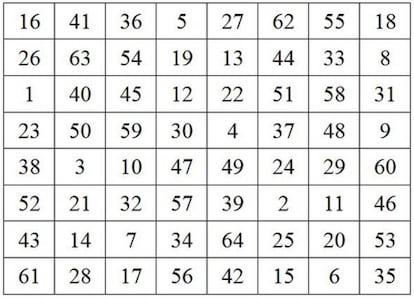
Sus filas, sus columnas y sus diagonales suman 260. Ahora, colocad en cada casilla el cuadrado de cada número y sumad ahora filas, columnas y diagonales. Correcto, todas suman 11180. Esto significa que estamos ante un cuadrado mágico que nos da otro cuadrado mágico al elevar todos sus términos a 2.

¿Pensáis que ya se ha acabado? Pues no, aún hay más. Echad un ojo a este cuadrado, creado porBenjamin Franklin:

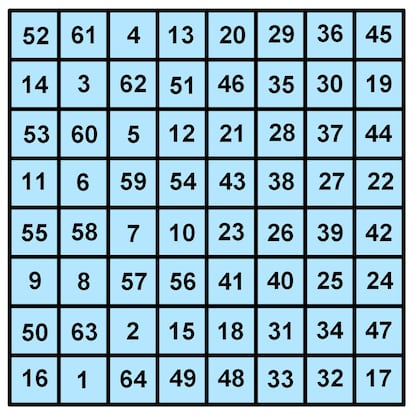
Si sumáis las filas y las columnas, el resultado es 260, pero las diagonales suman otro número. Pues tampoco es tan relevante como para citarlo aquí, ¿verdad? Bien, sumad las esquinas. Da 130, la mitad de 260. Sumad los cuatro números centrales, y también da 130. Ahora tomad cualquier cuadrado de cuatro números, el que queráis. Sumad sus elementos. ¿Resultado? Sí, 130. Y una más (posiblemente no la única). Si sumamos los cuatro elementos de la diagonal ascendente 50-8-7-54 y al resultado le sumamos lo que da la suma de los cuatro de elementos de la correspondiente diagonal descendente, 43-26-25-47, el resultado es 260. Bien, pues esto funciona en todos los casos, tanto si empezamos con ascendente y seguimos con descendente como si lo hacemos al contrario. Sencillamente genial.

Vamos ahora con uno más grande, de orden 13. Concretamente éste:

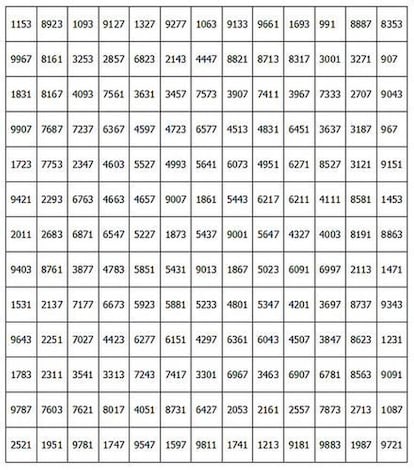
Su constante mágica es 70681. Tomad ahora el cuadrado de orden 3 central. Sumad filas, columnas y diagonales…Correcto, también es un cuadrado mágico. Chulísimo, ¿a que sí? Bien, tomad ahora el de orden 5 central…también es un cuadrado mágico. Y el de orden 7, y el de orden 9, y también el de orden 11. Increíble…

…y lo es aún más si sabemos que la constante mágica de cada uno de ellos difiere en 10874 respecto de la del anterior. Es decir, la del de orden 11 es 70681-10874=59807; la del de orden 9 es 59807-10874=48933; la del de orden 7 es 48933-10874=38059; la del cuadrado de orden 5 es 38059-10874=27185; y la del de orden 3 es 27185-10874=16311. Auténticamente asombroso.

Hemos visto cuadrados mágicos con números primos, algunos que mezclan distintas operaciones y otros con algunas propiedades realmente interesantes y curiosas, pero todos están relacionados directamente con números. ¿Con qué podían estarlo si no? Pues con la geometría. También hay cuadrados mágicos con figuras geométricas, llamados cuadrados geomágicos, como éstos:

En Geomagic Squares tenéis muchos más. Echadle un ojo, merece la pena.

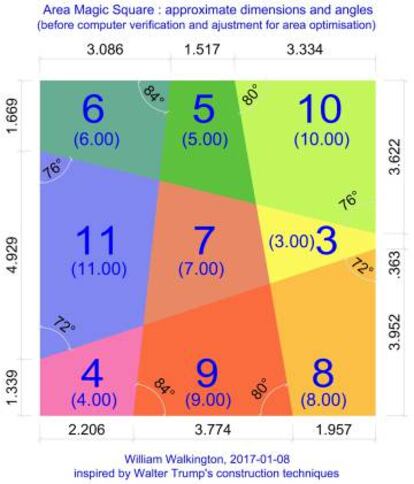
Para finalizar, os traigo el último tipo de cuadrado mágico del que he tenido conocimiento: el cuadrado de áreas mágicas. En él, cada región tiene de área el número que incluye, y el resultado da un cuadrado mágico habitual (filas, columnas y diagonales suman lo mismo). Aquí tenéis un ejemplo para que lo veáis mejor.

Una preciosa manera de relacionar los cuadrados mágicos numéricos con la geometría sobre la que podéis leer más en Area Magic Squares and Tori of Order-3.

Como habéis podido ver, el mundo de los cuadrados mágicos posee multitud de variantes, tanto numéricas como geométricas, y en este artículo he intentado mostraros algunas de ellas. ¿Algunas? Sí, porque eso es lo mejor de todo: aún hay mucho más en lo que se refiere a cuadrados mágicos: los hay alfanuméricos (como el que nos mostraba José Luis Carlavilla en este otro desafío), los hay reversibles (como el que nos enseñan aquí en Futility Closet) y los hay también creados a partir de fechas, que pueden dar juego utilizándolos con fechas de cumpleaños (como el que nos muestra Pedro Alegría en este pdf). Y mucho, mucho mucho más.

Por cierto, este artículo de Pedro Alegría que acabo de enlazar (muy recomendable) contiene otro cuadrado mágico que quiero destacar. Antes de que lo veáis, os cuento cómo construirlo. Tomad la fracción 1/19, realizad la división y quedaos con el período del número decimal resultante. Ahora haced lo mismo con 2/19, con 3/19, y así hasta 18/19. Colocad todos esos períodos por filas en ese orden y obtendréis un cuadrado mágico de constante mágica 81. Bellísimo, ¿verdad? Pues no es el único. Según nos comenta Pedro, también puede hacerse de manera similar con la parte periódica de 1/383.

Y, ya sí, concluyo este artículo divulgativo sobre el universo de los cuadrados mágicos con un vídeo dedicado al, posiblemente, más importante divulgador de las matemáticas de la historia: Martin Gardner. Disfrutad: