La maravillosa armonía que esconden los cuadrados mágicos

Lo confieso: soy un enamorado de los cuadrados mágicos. Y lo soy desde siempre, desde la primera vez que vi uno, desde el primer momento en el que tuve la fortuna de conocer la maravillosa armonía que esconden esas cajitas de números aparentemente colocados al azar. Aunque ahora mismo no sabría decir exactamente en qué momento de mi vida se produjo ese primer contacto con los cuadrados mágicos, mi fascinación por estos objetos matemáticos comenzó ahí y, puedo asegurar, continuará hasta el fin de mis días. Espero que con este artículo pueda contagiaros al menos una pequeña parte de este particular amor tanto a los que ya los conocéis como a los que no.

Definir cuadrado mágico es sencillo: es un cuadrado de números en el que todas las filas, todas las columnas y sus dos diagonales suman la misma cantidad, llamada constante mágica. Entre ellos, podría decirse que los más especiales son los que contienen una cierta cantidad de números enteros positivos consecutivos comenzando en el 1. Suponiendo que nuestro cuadrado mágico tiene n filas y n columnas, éstos serían los que contienen los números enteros positivos desde el 1 hasta el n². Por ejemplo, aquí tenéis uno de estos cuadrados mágicos con 4 filas y 4 columnas:

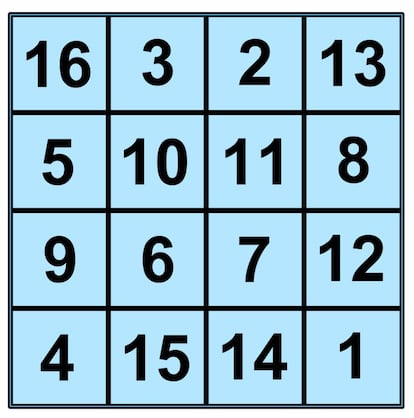
Podéis ver que todas las filas, todas las columnas y las dos diagonales suman 34, que sería entonces la constante mágica del cuadrado. En general, para estos cuadrados mágicos especiales tenemos una fórmula para calcular dicha constante mágica. Siendo n el número de filas y de columnas, esta constante es n(n²+1)/2.

Por cierto, éste no es el único cuadrado mágico de orden 4. De hecho hay 880 cuadrados mágicos de este tamaño (lo calculó Frenicle de Bessy en 1693). Por completar esto, hay un único cuadrado mágico de orden 1, no hay ninguno de orden 2 (¿sabrías demostrarlo?), hay solamente un cuadrado mágico de orden tres (salvo rotaciones y reflexiones) y exactamente 275305224 cuadrados mágicos de orden 5. Para órdenes superiores no se sabe con exactitud cuántos hay.

En lo que se refiere a su historia, simplemente comentaré que en el tercer milenio a. C. en China ya se conocían, y que otras civilizaciones antiguas como los egipcios, los griegos o lo árabes también tuvieron conocimiento de su existencia, atribuyéndoles habitualmente propiedades místicas. Según lo que sabemos, los cuadrados mágicos llegaron a Europa alrededor del siglo XIV, y muchos de los grandes matemáticos posteriores a esta fecha se interesaron por ellos.

Conocemos algoritmos para construir cuadrados mágicos de cualquier orden.

Pero dejemos hoy a un lado la historia y vayamos al turrón: ¿sabemos construir cuadrados mágicos? Esto es, ¿tenemos algún algoritmo mediante el cual podamos construir cuadrados mágicos? Pues sí, sabemos, y además podemos construir cuadrados mágicos de cualquier orden, aunque el método de construcción depende de cuál sea este orden.

Cuadrados mágicos de orden impar

Para este tipo de cuadrados mágicos se conocen varios métodos de construcción. El que aquí vamos a contar se denomina método de Loubère, y se debe al matemático francés Simon de la Loubère. Este método es como sigue:

Colocamos el 1 en la posición central de la fila superior, y después, a partir del 1 y en orden creciente, vamos colocando el resto de números en diagonal. Si en algún momento nos toca colocar un número en una posición ya ocupada, colocamos dicho número debajo del que habíamos colocado justo antes.

Como lo de la colocación en diagonal a veces puede ser algo liosa, os doy un truco: si un número se ha colocado en la posición de la fila p y la columna q, posición (p,q), el siguiente se coloca en la posición (p-1,q+1), teniendo en cuenta que si nos pasamos de n volvemos a 1 y bajamos de 1 volvemos a n. Si esa posición está ocupada, colocamos el número debajo de la posición (p,q).

Veamos cómo usar este método para construir un cuadrado mágico de orden 5. Comenzamos con el 1 en la posición (1,3); el 2 irá en la (5,4); el 3 en la (4,5); el 4 en la (3,1); el 5 en la (2,2); el 6 debía ir en la (1,3), pero como está ocupada (por el 1) lo colocamos debajo del 5, en la posición (3,2); el 7 iría ahora en la (2,3); el 8 en la (1,4); el 9 en la (5,5); el 10 en la (4,1); el 11 iría en la (3,2), pero ahí ya está el 6, por lo que lo colocamos debajo del 10, en la posición (5,1); y así sucesivamente. Nos quedaría el siguiente cuadrado mágico:

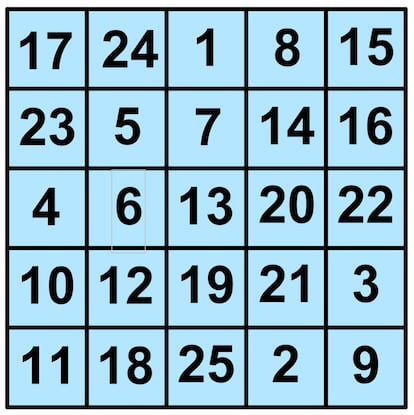
Podéis comprobar que todas las filas, todas las columnas y las dos diagonales suman 65, que es la constante mágica de estos cuadrados mágicos de orden 5.

Vayamos ahora con los de orden par. En este caso, debemos distinguir dos casos: los que tienen orden 4k (4, 8, 12, 16, 20…) y los que tienen orden 4k+2 (6, 10, 14, 18, 22…).

Cuadrados mágicos de orden 4k

Para construir este tipo de cuadrados mágicos, vamos a hacer lo siguiente:

Colocamos los números desde el 1 hasta el n por filas en orden creciente. Después, dejamos tal cual el cuadrado central de orden n/2 y los cuadrados de las esquinas de orden n/4.Y ahora intercambiamos los que quedan arriba con los que quedan abajo, colocándolos en orden decreciente, y los que quedan a la izquierda con los que quedan a la derecha, invirtiendo también el orden. El cuadrado resultante es un cuadrado mágico de orden 4k.

Por si la cosa no ha quedado muy clara, vamos a construir como ejemplo un cuadrado mágico de orden 8. A la izquierda podéis ver el cuadrado inicial, con los números colocados en filas en orden creciente y en el que hemos destacado los números que cambiaremos mediante un fondo amarillo (los que tienen fondo azul serán los que dejaremos donde están). A la derecha tenéis el cuadrado mágico que nos queda al intercambiar como hemos descrito antes:

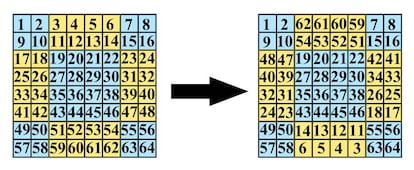
Cuadrados mágicos de orden 4k+2

Los métodos de construcción de estos cuadrados mágicos son algo más complejos. Como el artículo ya tiene bastante información, os dejo enlaces a dos de ellos para que quien esté interesado los pueda consultar:

· Método LUX, debido a John Horton Conway.

· Método Strachey.

Como comentábamos al principio del artículo, éstos cuya construcción hemos descrito son especiales porque llevar dentro de ellos números consecutivos a partir del 1. Pero hay muchos más, con números con características muy especiales y hasta con elementos que no son números. De ellos hablaremos en otra ocasión.

Y para finalizar este artículo sobre cuadrados mágicos, volvamos al 4x4 que os enseñaba unos párrafos más arriba:

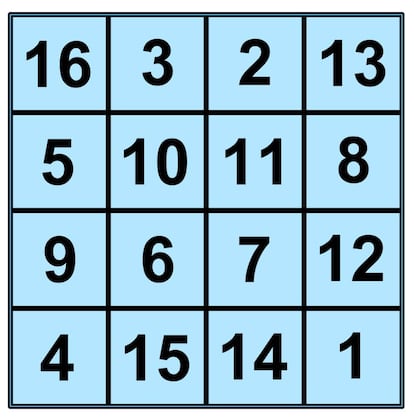
Este cuadrado mágico es muy famoso por aparecer en la obra Melancolía I de Alberto Durero, parte del cual ilustra este artículo. Aquí tenéis una imagen de la obra al completo:

Y es tremendamente interesante por muchas cosas. Como habíamos visto antes, la constante mágica de este cuadrado es 34: todas las filas, todas las columnas y las dos diagonales suman 34. Sumad las esquinas. Os da 34, ¿verdad? Sumad ahora los cuatro números centrales: da 34. Sumemos los dos centrales de la fila de arriba con los dos centrales de la fila de abajo: 34. ¿Y los dos centrales de la columna de la izquierda con los dos centrales de la columna de la derecha? Correcto: 34. Si lo dividimos en cuatro cuadrados 2x2, en todos los casos sus elementos suman 34, y hay muchas otras agrupaciones simétricas de números de cuatro en cuatro que, efectivamente, suman 34. Os animo a que las busquéis y a que nos lo contéis en los comentarios.

Espero que os haya gustado esta pequeña gran introducción a los cuadrados mágicos, y os invito a que intentéis construir algún otro con las reglas que hemos contado en este artículo. Si tenéis algún problema con estas construcciones no tenéis más que comentarlo. Y si conocéis algún otro método de construcción de cuadrados mágicos que no hayamos comentado aquí, estaremos muy agradecidos si nos lo queréis describir en un comentario. Muchas gracias a todos.