Pi, Indiana y legisladores con poco criterio
¿Puede alguna ley influir directamente en hechos demostrados matemáticamente? Quizás no debería, pero hubo un momento de la historia en el que estuvo a punto de hacerlo.

Creo que estaréis de acuerdo conmigo en que todo lo que gira alrededor de las leyes es complicado, tanto lo que se refiere a su creación como a su aplicación. La influencia que tienen sobre nuestra vida es tal que el “noble” arte de legislar conlleva una gran responsabilidad para quien tiene que “practicarlo”. Pero ello no impide que de vez en cuando nos topemos con alguna ley “peculiar”, por decirlo de alguna forma. En el mundo de internet aparecen de forma recurrente listas con algunas leyes que sin lugar a dudas podríamos calificar como absurdas. Por poner un par de ejemplos, parece ser que en Florida (EEUU) las mujeres solteras que salten en paracaídas los domingos pueden ser encarceladas; y en Reino Unido se considera acto de traición poner al revés un sello de correos en el que aparezca una imagen de la monarquía británica.
Bien, pues va a ser de esto de lo que vamos a hablar, No, de la monarquía británica no, de leyes absurdas. En concreto de un proyecto de ley que estuvo a punto de fructificar en Indiana a finales del siglo XIX con el que, básicamente, se habría conseguido legislar en contra de una verdad matemática ya demostrada.
Antes de entrar en la historia en sí, es fundamental dejar algo bien claro: la cuadratura del círculo con regla y compás es imposible. Quizás con la versión larga de esa afirmación la cosa se entienda mejor:
Dado un círculo del cual conocemos su radio, es imposible obtener un cuadrado cuya área sea la misma que la del círculo inicial utilizando regla y compás y las normas de utilización de estas dos herramientas que estaban aceptadas en la antigua Grecia para las construcciones ideales
Sin entrar en detalles, la razón por la que este problema no se puede resolver es que π (sí, el número Pi de toda la vida, 3,14159…) es un número de los llamados trascendentes (que son los números que no son solución de ningún polinomio cuyos coeficientes sean números enteros), hecho que fue demostrado en 1882 (repito, en 1882, quedaos con esto) por el matemático alemán Ferdinand von Lindemann.
Nuestra historia (cuya versión resumida comentaron en Verne hace unos meses) se sitúa en Indiana (EEUU) en el año 1897, cuando Edwin J. Goodwin, médico y matemático aficionado, le propuso al representante político Taylor I. Record un proyecto de ley, el número 246 de aquella sesión, cuyo título, agarraos a lo que tengáis a mano, acabó siendo el siguiente:
Un proyecto de ley que presenta una nueva verdad matemática y que es ofrecido como una contribución a la educación que sólo podrá ser utilizado por el Estado de Indiana en forma gratuita sin necesidad de pagar ningún tipo de royalties, siempre y cuando sea aceptado y adoptado en forma oficial por la legislatura en 1897
Dicho proyecto no era más que una demostración incorrecta del problema de la cuadratura del círculo (podéis ver su contenido aquí). Sí, en 1897, quince años después de que se demostrara que dicho problema no tenía solución.

El caso es que Record presentó el proyecto y la Casa de Representantes lo envío al Comité de Canales, que a su vez lo derivó al Comité de Educación. Éste último dio una opinión positiva sobre el mismo (¿?), por lo que la Casa de Representantes lo aprobó por unanimidad: 67 votos a favor y 0 en contra. El siguiente paso era el envío del proyecto número 246 al Senado para su más que probable aprobación (vistos los antecedentes) y, por tanto, su establecimiento como ley.
Y aquí es donde aparece el “héroe” de esta historia: Clarence Abiathar Waldo, matemático estadounidense. Waldo había acudido a gestionar el presupuesto anual de la Academia de Ciencias de Indiana cuando se enteró de que se estaba debatiendo un proyecto de ley relacionado con las matemáticas y se quedó a escuchar. La cara que se le debió quedar debió ser digna de inmortalizar para la posteridad.
Al finalizar el debate, uno de los Representantes le entregó una copia del proyecto y le ofreció presentarle al “genio” Goodwin. La respuesta de Waldo lo dice todo:
Ya conozco a tantos locos como puedo soportar
Pero, evidentemente, el bueno de Waldo no podía dejar que la historia quedara así. Esa misma tarde estuvo explicando a los Senadores el contenido del proyecto 246 y haciéndoles ver la barbaridad que aprobarían si votaban a favor del mismo. Y tuvo éxito, ya que consiguió convencer a un número suficiente de ellos para que no lo hicieran, quedando el proyecto pospuesto indefinidamente.
Por cierto, cuenta la historia que en aquella reunión en el Senado hubo tanto ridiculizaciones del proyecto como indignación por hacer gastar el dinero del ciudadano en tamaña frivolidad (aquí podéis encontrar todo lo que ocurrió el día de marras).
Acabada la historia (con final feliz, por suerte), queda por descubrir qué tiene que ver el proyecto 246 con el número Pi. De hecho, en el mismo ni se menciona dicho número, pero sí podemos encontrar en él la siguiente aseveración, consecuencia de la errónea resolución de Goodwin del problema de la cuadratura del círculo:
La razón entre el diámetro de una circunferencia y su longitud es cinco cuartos a cuatro
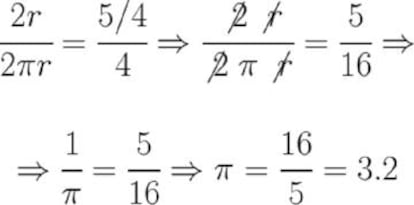
Si recordamos que dada una circunferencia de radio r su diámetro es 2r y la longitud de la misma es 2πr, esta frase nos da una expresión matemática de la que podemos despejar fácilmente el valor de Pi:
Es decir, la aprobación del proyecto 246 habría supuesto establecer por ley que el valor del número π es 3.2, y con ello, por ejemplo, su utilización en libros de texto de Indiana (gratis, eso sí) y el cobro de “derechos” por su uso fuera de dicho estado. Una aberración a todas luces.
Esperemos que los legisladores actuales mediten y debatan más sobre las leyes de lo que lo hicieron en aquel momento los de Indiana para que no se les “cuelen” barbaridades como ésta.
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.




























































