El problema de Alhacén

Con respecto al problema clásico de la mesa de billar a una o varias bandas, nuestro comentarista habitual Rafael Granero ha enviado un análisis exhaustivo que vale la pena reproducir entero:

Supongamos bolas de billar de radio 1. Supongamos la mesa de billar en un sistema de coordenadas donde el extremo inferior derecho de la mesa está en el punto (-1, -1) y el extremo superior derecho en el punto (n3 + 1, m3 + 1). Sabemos las coordenadas de los centros de la bola amarilla (n1, m1) y de la bola roja (n2, m2). Hagamos una imagen especular con respecto el eje de la Y (el eje está a una unidad de la banda inferior de la mesa), el centro de esta imagen estará en (-n2, m2).

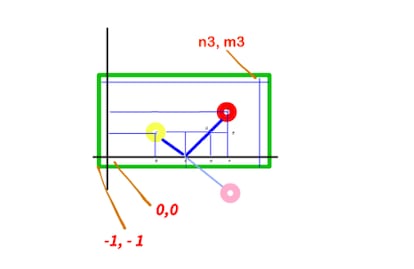
La ecuación de la recta que une a los centros de la bola amarilla y la imagen de la bola roja es:

(y2 - y1 )x - (x2 - x1)y + (x2·y1 - x1·y2) = 0

Y dado que el punto A tiene x = 0, entonces y = (-n2·m1 - n1·m2) / (-n2 - n1). Por otra parte, los triángulos ABC y AGD son iguales, y proporcionales a los triángulos AFH y DEH. Por lo que sabiendo la distancia del segmento HE y HF ([n2-n1] y [n2, respectivamente), sabemos la proporción entre los segmentos DE (y GF) con respecto AF.

También sabemos que el segmento BA = AG y que 2AG+GF = m2-m1, y que, por lo anterior dicho sobre los triángulos proporcionales AFH y DEH,

GF/(AG+GF)=(n2-n1)/n2

Despejando GF (o AG) podemos saber los valores de GF y AG (BA) y hallar el y de A (m1 + BA).

En el caso de dos bandas (inferior y derecha) primero hay que crear la imagen especular a la derecha (nuevas coordenadas (n2, 2·m3 - m2)) y luego la imagen especular hacia abajo (-2n, 2·m3 - m2), y con base en la ecuación de una recta que une dos puntos, volver a calcular la coordenada y del nuevo punto, ya que seguirá la x = 0.

En el caso de tres, será necesario tres imágenes especulares para ir convirtiendo una recta quebrada de cuatro segmentos en una recta de un único segmento… Y así, tantas bandas como queramos pensar.

Fotones como bolas de billar

Como se dijo la semana pasada, si planteamos el problema en una mesa de billar circular en lugar de rectangular y queremos averiguar en qué punto de la banda tendrá que incidir una bola para golpear de lleno la otra, tenemos una versión billarística del famoso problema de Alhacén.

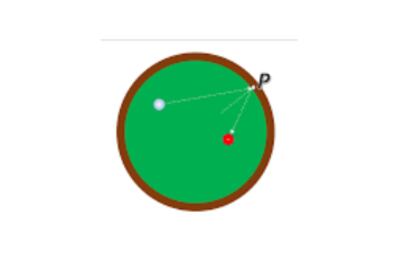
Es fácil ver que el punto P de incidencia de la bola atacante tendrá que ser tal que la bisectriz del ángulo que determinan los centros de las bolas con P sea perpendicular a la tangente en P (lo que equivale a decir que dicha bisectriz coincide con un diámetro de la mesa circular). Determinar dicho punto en función de las posiciones de las dos bolas ya no es tan fácil, y animo a mis sagaces lectoras/es a abordar el problema desde distintos ángulos (nunca mejor dicho): geométrico, algebraico… El problema se simplifica si ambas bolas están sobre un diámetro de la mesa: en ese caso hay una solución trivial, que consiste en lanzar una de las bolas contra la banda siguiendo el diámetro que determinan ambas, de forma que la bola atacante vaya y vuelva por el diámetro mismo; pero también hay otra solución (mejor dicho, dos simétricas), y hallarla es un primer paso para resolver el problema general, cuando las bolas no están sobre un mismo diámetro.

Pero Ibn al-Haytham (965-1040), conocido en Occidente como Alhacén, como corresponde a quien con toda justicia es considerado el padre de la óptica (y sobre todo de la catóptrica, la óptica de los espejos), no planteó su famoso problema sobre una mesa de billar, sino en el interior de un espejo circular, en el que el equivalente de las bolas de marfil son los fotones.

Imagínate que estás dentro de una habitación circular cuya pared es toda ella reflectante y que con el fino haz de un puntero láser quieres iluminar un objeto de la habitación, pero no directamente, sino haciendo que el rayo de luz se refleje en la pared: ¿con qué ángulo tendrás que dirigir el rayo para conseguir tu objetivo? Y una intrigante pregunta off the record: ¿cómo sería tu imagen reflejada en ese espejo circular envolvente?

Puedes seguir a MATERIA en Facebook, X e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.