Dodominós

Dos de las (parejas de) caras de los ortoedros cuyos lados están en la proporción 4:2:1 son dominós, por lo que, como pequeño homenaje a Lewis Carroll, estos dobles dominós podrían denominarse “dodominós” (Charles Dodgson solía tartamudear al decir su apellido: Do… Do… Dodgson; por eso se representó a sí mismo, en Alicia en el País de las Maravillas, como un pájaro dodo). Por lo tanto, nuestro tetrabrik ideal de las últimas semanas es un versátil dodominó de 20x10x5 cm.

Esta versatilidad permite recubrir con tetrabriks un tablero de ajedrez estándar de 40 cm de lado de muchas maneras distintas, si podemos apoyarlos sobre cualquiera de sus caras. Para empezar, podemos optar por 81 combinaciones distintas de caras, desde 8 caras de 20x10 hasta 32 caras de 10x5. Estas 81 combinaciones son las soluciones de la ecuación diofántica 8x + 4y + 2z = 64 (o lo que es lo mismo, 4x + 2y + z = 32), relativa, para simplificar, a dodominós de 4x2x1 sobre un tablero de 8x8, donde x, y, z son, respectivamente, los números de cada tipo de caras en cada una de las combinaciones posibles.

A su vez, cada combinación de caras permite un determinado número de recubrimientos distintos. Por ejemplo, con 8 caras de 4x2 podemos recubrir el tablero de 9 maneras diferentes, como muestra la imagen enviada por Salva Fuster.

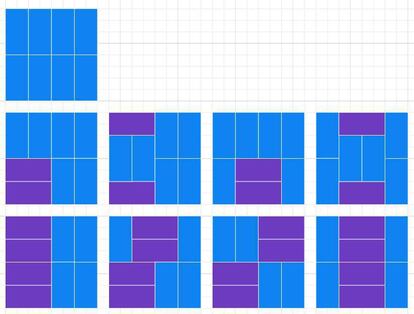
Las construcciones con dodominós en 3D planteadas en semanas anteriores siguen sin suscitar el interés de mis sagaces lectoras/es (pues no creo que rebasen sus capacidades analíticas), de modo que la cuestión sigue abierta.

Alquerque

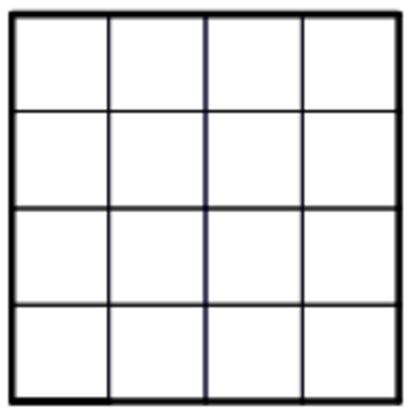
N 3122

S 2312

E 3132

O 2213

El tablero de 4x4 de la figura representa una manzana de edificios, uno por casilla. En cada línea, horizontal o vertical, los edificios son todos de distinta altura, y las alturas varían entre 10 y 40 metros. La tabla adjunta indica cuántos edificios son visibles desde cada dirección. Por ejemplo, si se mirara la secuencia de alturas 10, 40, 30, 20 de izquierda a derecha veríamos 2 edificios (los de alturas 10 y 40 metros) y mirando de derecha a izquierda veríamos 3 (los de alturas 20, 30 y 40 metros). En la tabla se indica el número de edificios que se ven desde cada lado (Norte, Sur, Este y Oeste) en cada columna y fila (las columnas se ordenan de derecha a izquierda y las filas de arriba abajo). Así, O 2213 significa que desde el lado izquierdo de la cuadrícula vemos 2 edificios en la primera fila, 2 en la segunda, 1 en la tercera y 3 en la cuarta. ¿Cuál es la distribución de los edificios?

Este problema tiene poco que ver, en principio, con nuestros dodominós; pero el Grupo Alquerque de Sevilla -un encomiable equipo de profesores de matemáticas preocupados por hacer más atractiva y comprensible para los alumnos la resolución de problemas- utilizó bloques de madera de 4x2x1 cm para resolver físicamente este y otros problemas similares.

Por cierto, ¿sabes lo que es el alquerque y qué relación tiene con los tableros de nxn casillas?

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.