Anna Kiesenhofer: del infinito al oro olímpico

En 2016 Anna Kiesenhofer defendió su tesis doctoral en la Universidad Politécnica de Cataluña (UPC), en un área de las matemáticas llamada geometría simpléctica. En 2021, el pasado 25 de julio, la matemática austriaca obtuvo, para la sorpresa de muchos, el oro olímpico en la prueba de ciclismo en ruta de los Juegos Olímpicos de Tokio. El grupo holandés, favorito en la competición, no supo contar las ciclistas que estaban en la escapada y, tras superar a la polaca Anna Plichta y a la israelí Omer Shapira, pensaron que no quedaba nadie más por delante; se olvidaron de Kiesenhofer. A pesar de este error, la ventaja y el empeño de la austriaca en los últimos kilómetros hubieran hecho muy difícil que la alcanzaran.

Tanto en su carrera deportiva como en la matemática, Kiesenhofer ha hecho gala de dos atributos fundamentales: disciplina y persistencia. Porque, por mucho que se empeñe Hollywood, en la vida real ni las grandes conjeturas se demuestran por inspiración divina, ni las medallas olímpicas se ganan por casualidad. Detrás de una victoria –deportiva o científica– se esconden también derrotas y adversidades, que es posible afrontar gracias a la resiliencia.

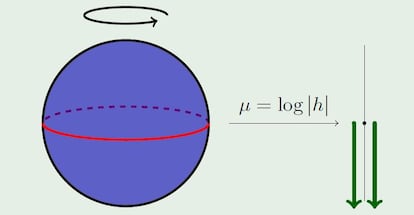
Anna Kiesenhofer estudió un doble grado de Matemáticas y Física en la Universidad de Viena y obtuvo su máster en Matemáticas en la Universidad de Cambridge. En 2012 llegó al Laboratorio de Geometría y Sistemas Dinámicos de la UPC para desarrollar su doctorado junto a Eva Miranda –coautora de este artículo– sobre un tipo de estructura, llamadas b-variedades simplécticas. En 2009, Miranda, junto con Victor Guillemin y Ana Rita Pires, había comenzado el estudio de estos objetos, motivada por el análisis de magnitudes métricas –como es el área– que tienden a infinito.

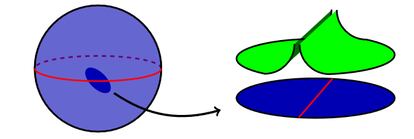
Imaginemos un globo terráqueo fabricado con chicle y cortado por el ecuador en dos partes; el resultado son dos superficies con borde, correspondientes al hemisferio norte y al hemisferio sur. Podemos estirar su borde ilimitadamente y el área de los hemisferios crecerá de la misma manera. En este caso, podríamos decir que la esfera –el objeto del que partíamos– admite una estructura de variedad b-simpléctica.

Las variedades b-simplécticas han resultado muy útiles para estudiar diversos problemas de la mecánica celeste, por ejemplo, para analizar colisiones de los cuerpos celestes. Conjuntamente con su directora, Anna Kiesenhofer estudió cierto tipo de sistemas –integrables– en estas variedades y sus perturbaciones.

Como casi todas las tesis aquella fue, de cierta manera, un pulso al infinito. Habitualmente, la persona que está realizando el doctorado debe resolver a uno o varios problemas en un periodo de tiempo acotado. Con ello se ejercita no solo el músculo matemático, sino también se aprende sobre la organización del trabajo investigador, identificando, peleando y disfrutando pequeñas y grandes metas. También es un periodo de aprendizaje introspectivo, en el que hay que hacer frente a las propias limitaciones y a las fortalezas.

Todo ello culmina con la defensa de la tesis, lo que para algunos supone un punto y final y para otros un preludio de la carrera investigadora. En el caso de Kiesenhofer, fue el principio de una trayectoria en la que combinaría dos de sus pasiones. Ese mismo año, en 2016, consiguió la victoria en la carrera general de la Copa de España de ciclismo y saltó a la fama internacional en el Tour Cycliste Féminin International de l’Ardèche, cuando coronó como ganadora el Mont Ventoux, quizás la cumbre más mítica, y quedó segunda en la final general.

Después de estos éxitos recibió varias ofertas de contratos y, en la temporada de 2017, compitió con el equipo del Lotto. Sin embargo, debido a problemas físicos que declaró estar padeciendo, no fue capaz de rendir como se esperaba, así que decidió retirarse y volver a las matemáticas. Ese mismo año obtuvo una plaza postdoctoral en la Escuela Politécnica Federal de Lausana (Suiza) para incorporarse al grupo de ecuaciones en derivadas parciales. Kiesenhofer y Miranda continúan su colaboración, estudiando simetrías generales en las variedades b-simplécticas.

En 2019 volvió a las competiciones ciclistas y ganó el Campeonato Austríaco Contrarreloj en los siguientes tres años, así como el de Ruta en 2019. En 2021, sin ningún patrocinio, ha competido por primera vez en los Juegos Olímpicos, en el equipo austriaco. Su victoria, como destacan los medios, ha requerido un derroche de fuerza y una perfecta dosificación de su ventaja en el circuito de Fuji. Fue una muestra de sus aptitudes físicas y mentales, pero también de su trabajo de entrenamiento, su excelente preparación y su afán de superación. Todas ellas, características que también definen su carrera matemática.

Manuel de León es Profesor de Investigación del CSIC en el Instituto de Ciencias Matemáticas (ICMAT) y académico de la Real Academia de Ciencias.

Eva Miranda es catedrática ICREA Academia de la Universidad Politécnica de Cataluña, miembro del Centre de Recerca Matemàtica y del Observatoire de París (Francia) e investigadora asociada al ICMAT.

Ágata Timón G-Longoria es coordinadora de la Unidad de Cultura Matemática del ICMAT y editora y coordinadora de esta sección

Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.