Siempre hay algún punto sin viento sobre la Tierra

En las previsiones meteorológicas de televisión suele mostrarse el mapa del viento. En ella aparecen sobre la Península una serie de flechas (vectores) superpuestas que indican la dirección y la intensidad del viento en el punto correspondiente. Si extendiéramos el mapa a toda la esfera podemos garantizar que en cualquier momento del día habrá al menos un lugar en el que no sopla nada de viento. Así lo determina el llamado teorema de la bola peluda, demostrado a principios del s. XX.

Matemáticamente, el mapa del viento corresponde a un campo de vectores sobre una superficie. Éste asigna a cada punto de la superficie un vector tangente a la misma, de tal modo que puntos cercanos tienen asociados vectores parecidos, tanto en dirección como en longitud. A algunos puntos de la superficie se puede asignar el vector de longitud cero: serán los puntos críticos del campo de vectores. En el ejemplo meteorológico, esos serían los lugares donde no sopla el viento.

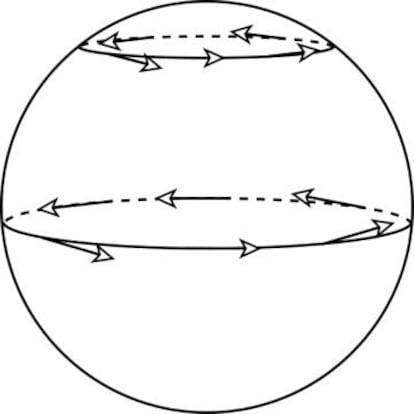
Sobre el mapa de España es fácil dibujar un campo de vectores sin puntos críticos: por ejemplo, podríamos asignar a cada punto una flecha que apunte al Este. Pero al extender este campo a la totalidad de la superficie de la Tierra (ver ilustración 1), el polo norte y el polo sur serían puntos críticos. En efecto, en ambos polos habría que buscar un vector con una dirección parecida a la de los vectores cercanos, pero en los paralelos más próximos hay vectores que apuntan en infinitas direcciones distintas, así que para cumplir las condiciones establecidas solo es posible tomar un vector de longitud cero.

De hecho, para cualquier campo definido sobre la esfera, aparecerá al menos un punto de este tipo. Esta afirmación se conoce de forma popular como el Teorema de la Bola Peluda, y es habitualmente interpretado diciendo que, no importa cómo se peine una cabeza, siempre aparece un remolino. ¡Algo que, cualquiera que haya peinado alguna vez a un/a niño/a, sabe a la perfección! Es consecuencia de uno de los resultados más importantes de la topología diferencial, el teorema de Poincaré-Hopf, demostrado por el francés Henri Poincaré en el caso de superficies y generalizado por Heinz Hopf a espacios de mayor dimensión.

El teorema de Poincaré-Hopf determina, de forma general, sobre qué tipo de espacios es posible construir un campo de vectores sin puntos críticos. En concreto se aplica a superficies cerradas, es decir, aquellas que se pueden deformar (sin cortar ni pegar) en una esfera con un número finito (que también puede ser cero) de asas, o agujeros. Relaciona conceptos matemáticos a priori diferentes: el campo de vectores y la forma intrínseca (la topología) de una superficie.

Según el teorema, dado un campo de vectores con un número finito de puntos críticos sobre una superficie cerrada con g asas los índices de todos los puntos críticos suman exactamente 2 – 2g. El índice de un punto crítico de un campo de vectores es un número entero distinto de cero que describe el comportamiento del campo de vectores en puntos muy próximos al punto crítico en cuestión.

En el caso de la esfera (que tiene cero agujeros), el teorema asegura que, para cualquier campo de vectores, la suma de los índices de todos los puntos críticos es 2. Por tanto, al menos tiene que haber uno ya que, evidentemente, si no hubiera ninguno, la suma sería cero. En general, excepto para las superficies cerradas con una sola asa, la suma siempre será distinta de cero, y por tanto cualquier campo vectorial definido sobre ellas tendrá algún punto crítico. El caso de un agujero se corresponde con el donut (llamado toro, en matemáticas). Aplicando el teorema sabemos que la suma de los índices de los puntos críticos de cualquier campo vectorial es siempre cero. Esto no garantiza que haya alguno sin puntos críticos, pero tampoco lo impide, como sucede en el resto de casos.

De hecho, sí es posible definir un campo sin puntos críticos sobre el toro. Para ello dibujamos, primero, un campo de vectores sin puntos críticos sobre una circunferencia (ver los círculos marcados en la ilustración 1). Como el toro es el resultado de rotar una circunferencia en el espacio tridimensional, basta rotar el campo que habíamos dibujado la circunferencia para obtener uno del toro. Por tanto, y por si alguien se había planteado la pregunta: sí, es posible peinar un donut sin que quede ningún remolino. 

Javier Aramayona es investigador Ramón y Cajal en la Universidad Autónoma de Madrid y miembro del ICMAT.

Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: "Un matemático es una máquina que transforma café en teoremas".

Edición y coordinación: Ágata Timón (ICMAT).