¿Puede ser una pésima idea ir en coalición?

Llegamos al tercero y último de los desafíos matemáticos que EL PAÍS y la Real Sociedad Matemática Española están proponiendo con motivo del periodo electoral. Como los anteriores, lo presentan, Angélica Benito Sualdea y Adolfo Quirós Gracián, profesores de Matemáticas en la Universidad Autónoma de Madrid.

El desafío trata sobre la diferencia entre los resultados electorales que conseguiría una coalición y los que alcanzarían los partidos por separado. Los lectores pueden enviar sus respuestas hasta las 00.00 del lunes 20 de mayo (la medianoche del domingo al lunes, hora peninsular española) a problemamatematicas@gmail.com.

A continuación, para aclarar dudas, añadimos el enunciado del problema por escrito.

En España la mayoría de los procesos electorales se rigen por el método D'Hondt, cuyo funcionamiento explicamos en el desafío anterior. Veamos qué sucede, usando el método D'Hondt, si dos partidos deciden ir en coalición bajo la hipótesis (no del todo realista) de que todos los votantes que fuesen a optar por uno de ellos votan a la coalición.

Puede ser que la coalición obtenga los mismos escaños que habrían obtenido los partidos por separado. Por ejemplo, si hay que repartir 3 escaños entre 3 partidos que han obtenido respectivamente 100, 100 y 70 votos, tenemos la siguiente tabla:

Como 70>50, D'Hondt asigna un escaño a cada partido.

Si los dos partidos mayores van en coalición y suman los votos:

obtendrán 2 escaños, pero no más, porque 100>70 pero 66,6<70.

También puede ser que la coalición gane escaños.Por ejemplo, si en una elección como la que acabamos de explicar los votos fuesen 105, 105 y 60, la situación sería:

Por separado, cada partido obtiene un escaño.

Pero ahora, si los dos partidos mayores suman sus votos tenemos:

y, como 70>60, la coalición se llevarían los 3 escaños, quitándole al partido C el que ganaba.

Lo que no puede pasar es que una coalición obtenga menos escaños que los partidos por separado (insistimos, bajo la hipótesis de que todos los votantes que fuesen a optar por uno de ellos votan a la coalición), y uno de los motivos para elegir el método D'Hondt cuando se celebraron las primeras elecciones democráticas en 1977, un momento en el que España había lo que se conocía como "sopa de letras de partidos", fue precisamente que incentiva las coaliciones.

Demostremos ahora que la coalición no pierde escaños. Supongamos que el partido A ha obtenido u votos y n escaños, y el B ha obtenido v votos y m escaños.

Llamemos q al último cociente que ha obtenido escaño.

Tenemos entonces:

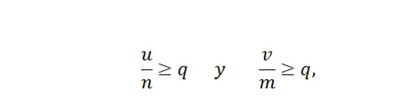
o, lo que es lo mismo

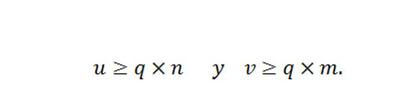
Sumando ambas desigualdades se tiene

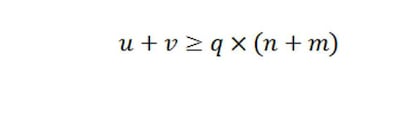
y, por tanto,

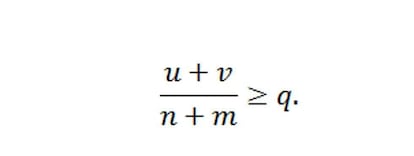
Esto muestra que, como q era el punto de corte para obtener escaños, y los votos de los demás partidos no han cambiado, una coalición de A y B que sumase todos los votos obtendría al menos n+m escaños antes de llegar al último cociente q. Podría obtener más, como muestra el ejemplo anterior, pero no menos.

El desafío que proponemos consiste en analizar qué puede suceder con una coalición si, en lugar de D'Hondt utilizásemos otro método que se ha propuesto en algún momento para su uso en España: el de Sainte-Laguë. Funciona de manera similar al de D'Hondt, pero dividiendo los votos sólo entre 1, 3, 5, 7,… (por eso se llama también método de los divisores impares).

Los lectores tienen que decidir si, usando el método de Sainte-Laguë, dos partidos que se presenten en coalición y que reciban los votos de todos los que habrían votado a cada uno de ellos, pueden obtener los mismos escaños, ganar escaños o perder escaños con respecto a la suma de los que habrían logrado por separado.

Para cada una de las tres posibilidades hay que, como hemos hecho nosotros para D`Hondt, o bien dar un ejemplo en el que se produzca, o bien dar una demostración de que no puede producirse.