Conectando ciudades sin cortarse

Por razones que ahora no son importantes, quiero tener la posibilidad de viajar de manera directa desde Puertollano a Valdepeñas, Manzanares y Villanueva de los Infantes cuando la ocasión lo requiera. Conozco a alguien que quiere tener la misma posibilidad, pero viaja desde Ciudad Real, y ambos sabemos de otra persona que desea tener la misma opción, pero partiendo de Tomelloso. La situación de todas estas ciudades en el mapa la podéis ver en la siguiente imagen:

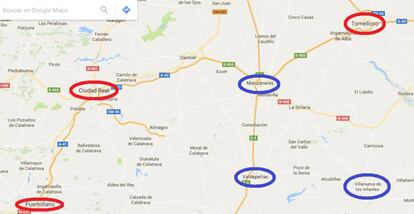
Es fácil crear caminos directos entre las ciudades que queremos conectar, pero hay una condición a tener en cuenta en este caso: no nos queremos encontrar. No nos llevamos bien y no queremos que se dé el caso de que nos encontremos por la carretera en ninguno de nuestros viajes, aunque eso suponga tener que hacer más kilómetros de los necesarios. Por tanto, las carreteras que deberían construirse no pueden cortarse. Suponiendo que ninguna se construye de forma elevada (vamos, que todas van por el suelo), ¿cómo podríamos resolver este problema?

Bien, quizás ordenando un poco las ciudades las cosas se vean mejor. Vamos a representar cada una de ellas con un punto y cada una de las carreteras con una línea. Dibujándolas todas como segmentos, la cosa quedaría así:

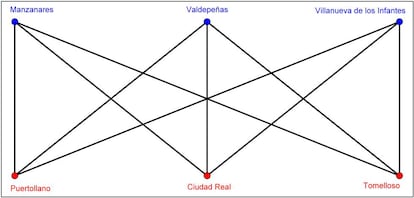
Como podéis ver, en esta imagen las carreteras se cortan. La idea es que no se corten, por lo que habría que dibujar alguna de las carreteras de otra forma (curva, poligonal…). Os dejo que las dibujéis como queráis. Venga, papel y lápiz y a dibujar un ratito antes de seguir leyendo.

Seguro que a más de uno le suena este problema como el problema de las casas y los suministros, en el que se desea conectar tres casas con los suministros de luz, agua y gas sin que las conexiones entres casas y suministros se corten entre sí. Y seguro que muchos os habéis dado cuenta de que, al representar las ciudades con puntos y las carreteras con líneas, la situación hipotética (o no, vete tú a saber…) que describíamos en los primeros párrafos nos ha llevado de un problema “geográfico” a un problema de teoría de grafos, teoría de la cual ya hemos hablado en este blog aplicada a la “adivinación” de la letra del DNI y cuando estudiamos cuándo se podían hacer dibujos en un solo trazo.

¿Ya lo habéis intentado? ¿Qué tal ha ido la cosa? Voy a intentar adivinar: no habéis conseguido lo que os pedía. Si es así, podéis estar tranquilos, ya que no se puede hacer lo que os he os requería al principio (si pensáis que lo habéis conseguido, os recomiendo que reviséis vuestro dibujo, seguro que hay algo mal). Como mucho, podemos conectar dos ciudades de uno de los grupos (el rojo, por ejemplo) con las tres del otro grupo y conectar la tercera ciudad del primer grupo con dos del otro grupo, pero nos faltaría una carretera que colocar y ya no tendremos opción de evitar que corte con alguna de las ya colocadas. En la imagen tenéis un ejemplo de ello:

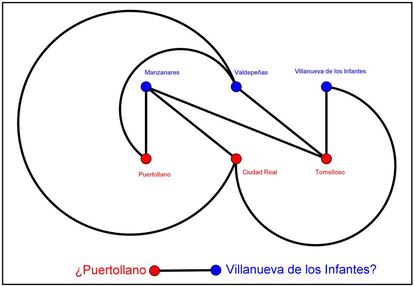
Para explicar la imposibilidad de realizar esta construcción, vamos a meternos de lleno en teoría de grafos. El grafo que representa la situación que planteábamos, el que aparece en la primera imagen, se conoce como K_3,3. Su definición es precisamente la que ilustra nuestro problema: dos grupos distintos de tres vértices cada uno (sin vértices comunes) tal que cada uno de los de un grupo está conectado solamente con los tres del otro grupo. Es un caso particular de los grafos tipo K_m,n, que se definen de manera análoga.

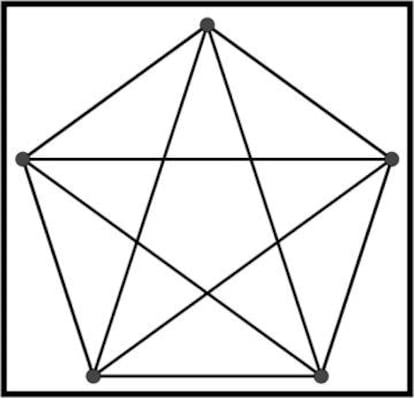
Lo que asegura que nuestra construcción es imposible es que está demostrado que este grafo no es plano (un grafo es plano cuando cualesquiera dos aristas se cortan solamente en un vértice o no se cortan), y también está demostrado que K₅ (el grafo de cinco vértices en el que cada vértice está conectado con los otros cuatro) tampoco es plano.

¿A cuento de qué introducimos ahora el grafo K₅ en el juego? Aunque parece que no tiene mucho que ver con nuestro K_3,3, en realidad están muy relacionados. Ambos grafos son los protagonistas del conocido como teorema de Kuratowski, demostrado por el matemático polaco Kazimierz Kuratowski en 1930. Dicho teorema dice lo siguiente:

“Un grafo es plano si y sólo si no contiene ningún subgrafo que sea una subdivisión elemental de K_3,3 o de K₅.”

Como no merece la pena entrar ahora en detalles en lo que respecta a eso de subdivisión elemental, vamos a dejar el teorema en que un grafo es plano si no contiene una parte que sea esencialmente igual que K_3,3 o que K₅. Es decir, este teorema nos dice, sin ninguna duda, si un grafo es plano o no lo es (es, por tanto, una caracterización de los grafos planos). En nuestro caso, como es el propio K_3,3, el grafo que representa las carreteras por las que queremos viajar no es un grafo plano, por lo que si queremos hacer lo que pedíamos en los primeros párrafos no tenemos otra opción que dejar al menos un punto de intersección en el que, aunque no nos guste, corremos el peligro de encontrarnos.

Y nos da igual lo grande que sea el grafo en lo que a vértices y aristas se refiere: si hay K_3,3 o K₅, el grafo no es plano; y si no encontramos a ninguno de ellos, entonces el grafo sí es plano. Otra cosa es lo fácil o difícil que sea encontrar alguno de estos grafos de Kuratowski (sabéis ya de dónde viene la K que aparece en el nombre de estos grafos, ¿verdad?) dentro de un grafo muy grande y complejo, pero eso ya es otra cuestión.

En este artículo, además de presentaros el concepto de grafo plano y a los grafos de Kuratowski, quería mostraros lo sencillo que es traspasar un problema real a la teoría de grafos, y lo útil que es esto a la hora de estudiar dicho problema. Actualmente, la teoría de grafos es una de las teorías matemáticas con más aplicaciones prácticas, y una de las que más resultados interesantes (tanto resueltos como sin resolver) posee.

Seguro que vosotros conocéis más situaciones concretas en las que la teoría de grafos nos nos aporta soluciones. Si queréis compartir esas aplicaciones prácticas con nosotros, los comentarios (como siempre) son vuestros.