Lord Kelvin, Pekín 2008 y un monólogo de humor

Las abejas tienen habilidades matemáticas. Esto ya lo destacó Pappus de Alejandría en el siglo IV cuando analizó la forma en la que estos insectos construyen sus panales.

Además de por construir las celdas con un ángulo final óptimo, la forma hexagonal de las celdas no parece ser ni mucho menos casual, ya que el hexágono regular es el polígono que, a igual área, tiene menor perímetro, por lo que es el mejor para rellenar, o teselar, un plano con polígonos (es decir, para construir panales óptimos). Fue precisamente Pappus quien conjeturó este resultado, pero no lo demostró.

Y así se mantuvo la cosa, sin demostración, hasta 1999, año en el que Thomas Hales demostró la veracidad de la conocida como conjetura del panal en su trabajo The Honeycomb Conjecture, cerrando así el círculo: efectivamente, entre todos los polígonos (sean convexos o no convexos) el hexágono regular es el polígono más eficiente para rellenar un plano.

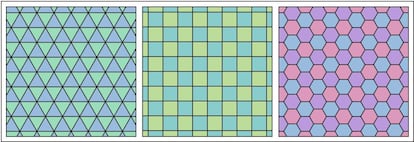
A partir de esto, surge de manera natural el hecho de preguntarse qué ocurre en tres dimensiones. La pregunta, en este caso, sería la siguiente: ¿cuál es el poliedro que, a igual volumen, tiene menor área? O dicho de otra forma: ¿cuál es el poliedro más eficiente para rellenar el espacio tridimensional con él?

A finales del siglo XIX, Lord Kelvin conjeturó que sería el octaedro truncado.

El propio William Thomson (que era el verdadero nombre de Lord Kelvin) estableció esta conjetura en su trabajo On the division of space with minimum partitional area (que podéis descargar en pdf). Esto es lo que motivó que este problema se denominara, a partir de ese momento, conjetura de Kelvin. En la siguiente imagen podéis ver cómo quedaría un rellenado del espacio tridimensional con estos preciosos poliedros, los octaedros truncados:

Pero, como ocurrió en el caso anterior con Pappus, Lord Kelvin no pudo demostrar que el octaedro truncado era el poliedro más eficiente entre todos los poliedros que son capaces de rellenar el espacio tridimensional. Era el mejor resultado conocido, pero no se sabía si era el más eficiente.

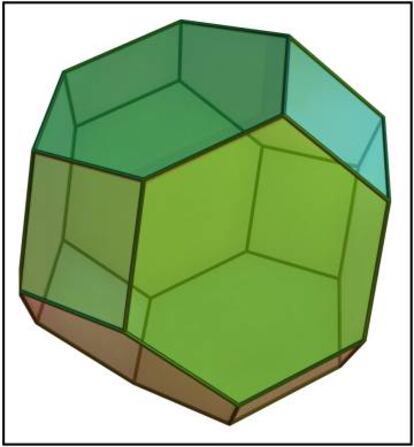
El problema se mantuvo así hasta finales del siglo XX. En 1994, Denis Weaire y Robert Phelan publican el trabajo A counter-example to Kelvin’s conjecture on minimal surfaces. En él, como indica su propio título, Weaire y Phelan presentan un contraejemplo a la conjetura de Kelvin dando un poliedro que es más eficiente que el octaedro truncado a la hora de rellenar el espacio con él. Dicho poliedro, conocido actualmente como estructura de Weaire-Phelan (sí, un nombre muy original e imaginativo…), está formado por dos dodecaedros irregulares con caras pentagonales y seis tetradecaedros con dos caras hexagonales y doce caras pentagonales y, según el trabajo de Weaire y Phelan, es un 0’3% más eficiente que el octaedro truncado. Aquí tenéis una imagen de esta estructura:

Bonita, ¿verdad? Bonita y aparentemente complicada de montar. Quien esté interesado en montarla puede visitar este enlace de CutOutFoldUp, donde podrá encontrar distintas plantillas y los pasos necesarios para montar la estructura de Weaire-Phelan. Por cierto, esta web contiene muchísimas plantillas e información para construir en papel una gran cantidad de figuras. Muy recomendable para los amantes de estas construcciones.

¿Podría tener esto alguna aplicación práctica? Pues sí, la tiene: construcciones. En los Juegos Olímpicos de Pekín en 2008 pudimos ver una construcción basada en esta estructura: el Beijing National Aquatics Center:

Bien, entonces problema resuelto, ¿verdad? Pues no. Weaire y Phelan encontraron una estructura más eficiente que el poliedro de Kelvin, pero no demostraron que fuera la más eficiente. Es decir, es más eficiente que el octaedro truncado pero no se sabe si es la mejor posible, por lo que podría encontrarse una estructura poliédrica más eficiente que la de Weaire-Phelan. O también podría demostrarse que, efectivamente, sí que es la mejor posible. A día de hoy seguimos sin saberlo, pero esperamos vivir lo suficiente como para poder contarlo.

Quien recuerde el título de este artículo se estará preguntado qué tiene que ver un monólogo de humor con todo esto. Pues lo explico ahora mismo. FameLab es un certamen de monólogos científicos cuyo objetivo es explicar conceptos de ciencia, tecnología o ingeniería mediante monólogos de tres minutos. En 2013 se celebró la primera edición de FameLab España, y el ganador fue el matemático Eduardo Sáenz de Cabezón (quien, dicho sea de paso, actualmente mantiene Derivando, un muy recomendable canal de YouTube en el que publica vídeos sobre matemáticas). El monólogo con el que ganó se titulaba Un teorema es para siempre, y en él hablaba sobre este tema de la conjetura del panal y la conjetura de Kelvin.

Creo que la mejor forma de terminar este artículo es, precisamente, disfrutar del monólogo ganador de Eduardo. Aquí lo tenéis: