Particiones y repartos

En el problema de la esfera de la semana pasada parecen faltar datos, pero la solución es única. Por las condiciones del problema, tanto 4r² como 4r³/3 han de ser números enteros de cuatro cifras, o sea, comprendidos entre 1.000 y 9.999, por lo que 20 > r > 15, y como ha de ser entero, r solo puede tomar los valores 16, 17, 18 o 19. Por otra parte, para que 4r³/3 sea entero, r ha de ser divisible por 3, por lo que la única posibilidad es r = 18.

¿Y si en vez de cuatro cifras ambos números enteros tuvieran cinco? ¿Se puede generalizar a n cifras?

En cuanto al triángulo obtusángulo a dividir en acutángulos, es fácil llegar a la falsa conclusión de que es imposible (Martin Gardner contaba que en su día recibió varias “demostraciones” de tal imposibilidad), pues por mucho que lo dividamos siempre acaba quedando al menos un pequeño y obstinado obtusángulo, como el del vértice inferior derecho de la figura.

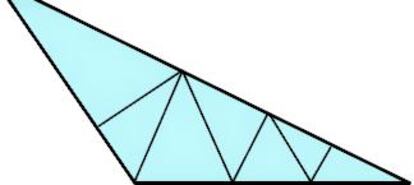
Sin embargo, la división es posible, y como pista diré que es uno de esos instructivos problemas en los que, inconscientemente, nos ponemos más condiciones de las que nos piden. El más conocido de estos acertijos es el de los nueve puntos en cuadrícula que hay que unir con solo cuatro trazos rectilíneos sin levantar el lápiz del papel, y del que hemos hablado más de una vez en esta sección.

En este caso, la condición autoimpuesta es la de que los vértices de la línea quebrada de la solución coincidan con sendos puntos de la cuadrícula.

Hay numerosos problemas verbales de este tipo, que a veces ponen en evidencia arraigados prejuicios. Un ejemplo clásico:

Una joven y su padre sufren un accidente de automóvil. El padre muere en el acto y a la chica hay que operarla de urgencia. La trasladan al hospital más cercano, pero quien debería realizar la delicada operación pide que la lleve a cabo otra persona, alegando que la víctima es su hija. ¿Cómo es posible, si el padre acaba de morir en el accidente? Muy sencillo: la cirujana es la madre de la chica. (En inglés queda mucho mejor, al jugar con la ambigüedad del término doctor).

En cuanto al palíndromo 121121, derivado de la fecha de publicación de la entrega anterior (12 11 21), es un supercapicúa: además de estar formado por dos 121 (que a su vez es el cuadrado de 11, el menor de los capicúas), 121121 = 33³ + 44³, la suma de los cubos de dos capicúas consecutivos. Y por si esto fuera poco, 121121 = 66³ – 55³, la diferencia entre los cubos de otros dos capicúas consecutivos entre sí y consecutivos de los dos anteriores.

Quien parte y reparte…

Un triángulo obtusángulo dividido en acutángulos, una esfera dividida por un plano (ver entrega de la semana pasada), un capicúa descompuesto en cubos… Sigamos, pues, con el interesante asunto de las particiones.

Preguntaba recientemente un lector en cuántas partes se puede dividir una pizza con 1, 2, 3, 4… cortes rectilíneos. Es evidente que con un corte solo se puede dividir en dos partes, con dos cortes en cuatro, con tres cortes en siete… (¿Y un bizcocho? Pero ¿tiene sentido diferenciar entre una pizza y un bizcocho?). ¿Se puede generalizar el problema a n cortes?

Para evitar que el que parte y reparte se lleve la mejor parte, hay un procedimiento sencillo, cuando las partes son dos, para lograr que ambos se queden satisfechos: uno parte y el otro elige, con lo que el primero pone buen cuidado en que las partes sean iguales. Pero ¿y si son tres las personas que desean repartirse algo de forma equitativa? ¿Y si son cuatro, cinco, seis…?

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.