Dominar el dominó
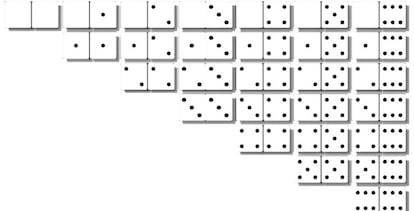
¿Cuántas cadenas distintas se pueden formar con las 28 fichas de dominó?
Hay distintas maneras de abordar el problema de las banderas planteado la semana pasada, y tal vez la más sencilla sea considerar que la franja central puede ser de cualquiera de los 6 colores y en cada caso tenemos 5 opciones para cada franja lateral (pues dos franjas adyacentes no pueden ser del mismo color, ya que en tal caso se convertirían en una sola franja de doble anchura); en total, 6 x 5 x 5 = 150 banderas de tres franjas verticales y otras tantas de tres franjas horizontales.
Cabría objetar que la bandera azul/blanca/roja es la misma que la roja/blanca/azul, y así es si las consideramos rectángulos de tela sueltos, pues una es el reverso de la otra (o la otra girada 180º); pero las banderas siempre se unen al mástil por el mismo color en el caso de las de franjas verticales, y siempre se sitúan con el mismo color arriba en el caso de las de franjas horizontales. Así, la bandera francesa es azul/blanca/roja (empezando a partir del mástil), distinta de una hipotética bandera roja/blanca/azul; y la bandera alemana es negra/roja/amarilla (empezando por arriba), y no amarilla/roja/negra.
Pasar o no pasar, esa es la cuestión
La combinatoria de letras y colores dio paso, en la animada sección de comentarios, a la de las fichas de dominó, y un problema aparentemente sencillo originó un interesante debate (ver comentarios de las dos últimas semanas). Este es el problema, por si alguien quiere retomarlo: En una partida de dominó convencional (cuatro jugadores con siete fichas cada uno), el jugador que está a tu izquierda abre con el seis doble y tú pasas. ¿Has tenido muy mala suerte o era relativamente probable que te ocurriera?
Y aprovechando que tenemos las fichas sobre la mesa, veamos otro problema en cierto modo opuesto al anterior (en vez de pasar a la primera de cambio, ahora nadie pasa en ningún momento):
¿Cuántas cadenas distintas (respetando las reglas del juego) se pueden formar con las 28 fichas de dominó? O dicho de otro modo: ¿Cuántas partidas distintas se pueden jugar sin que nadie pase? (En puridad, la partida se acabaría cuando el jugador que abrió colocara su última ficha; pero vamos a suponer que los otros tres también terminan de colocar las suyas).
Suponiendo que falte una ficha, ¿se puede, y en qué casos, formar una cadena continua con las 27 restantes? Y una vez formada la cadena, ¿cómo se puede identificar fácilmente la ficha faltante?
Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos Maldita física, Malditas matemáticas o El gran juego. Fue guionista de La bola de cristal.
Sobre la firma
