Pensamiento mecánico

Las soluciones numéricas del problema de las ocho damas, propuesto la semana pasada, han de cumplir la condición de que la diferencia entre dos dígitos cualesquiera no sea igual a la “distancia” entre ellos, entendiendo por tal el número de lugares que están alejados el uno del otro, pues de lo contrario corresponderían a dos damas situadas en la misma diagonal.

Un despiste de última hora me llevó a colgar como ilustración de portada la solución en la que no hay tres damas alineadas. Sin contar giros y rotaciones, creo que es única; su notación numérica: 3584126 (recordemos que cada dígito indica la fila ocupada correspondiente a cada columna, de izquierda a derecha).

Para abarcar todo el tablero son necesarias y suficientes cinco damas. Una de las soluciones consiste en colocarlas en la diagonal del tablero de la forma 80654020 (los ceros corresponden a las columnas en las que no hay dama). En la figura vemos otra de las 4.860 soluciones posibles (85746000).

Cinco damas también son suficientes para abarcar tableros de 9x9, 10x10 y 11x11 (aunque en este caso las casillas ocupadas no están necesariamente a tiro de otras damas). Una solución en el tablero de 11x11: 040X0602080 (la X representa la fila 10).

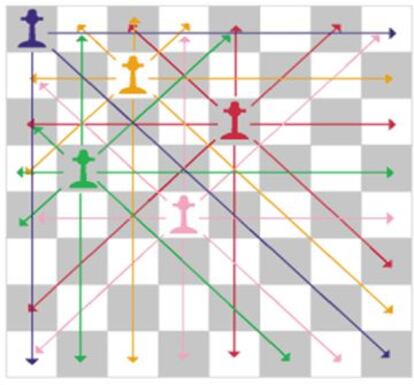
Puesto que no puede haber dos torres en una misma fila ni en una misma columna, es evidente que el máximo número de torres que podemos colocar en un tablero sin que ninguna amenace a ninguna otra es ocho. Para calcular todas las disposiciones posibles, empecemos situando una torre en la primera columna; tenemos 8 posibilidades, para cada una de las cuales tenemos 7 posibilidades al situar otra torre en la segunda columna, y para cada una de estas 8x7 parejas tenemos 6 posibilidades al situar la torre en la tercera columna… El número total será, pues, 8x7x6x5x4x3x2x1, o sea, 8! = 40.320.

Tres sombreros blancos

Es interesante comparar el problema de las ocho damas con el análogo pero mucho más sencillo de las ocho torres: en el segundo caso es fácil hallar una fórmula que nos da el número de soluciones para tableros de cualesquiera dimensiones, mientras que en el primer caso no es en absoluto así. Con algunos acertijos lógicos aparentemente simples ocurre algo similar: se resisten a ser abordados pensando de forma lineal y mecánica, y requieren, para su resolución, seguir procesos ramificados, reticulares o que incluyen curiosos bucles. Un ejemplo clásico y relativamente sencillo (pero no os confiéis) es el siguiente:

Un rey decide indultar a uno de los tres prisioneros que están encerrados en las mazmorras de palacio. Los llama a su presencia y les dice: “En este cofre hay tres sombreros blancos y dos negros. A cada uno de vosotros le pondrán uno de estos cinco sombreros, de modo que cada cual verá los que llevan los demás, pero no el que lleva él mismo ni los que han quedado en el cofre. El que deduzca de qué color es el sombrero que lleva y justifique su conclusión quedará en libertad”. Tras unos instantes de reflexión, el primer prisionero afirma que no puede saber de qué color es su sombrero, y el segundo dice lo mismo; y entonces el tercero dice: “Mi sombrero es blanco”. ¿Cómo lo sabe?