El problema de las ocho damas

El problema de las ocho damas, propuesto la semana pasada, fue planteado por primera vez por el ajedrecista alemán Max Bezzel, que, con el seudónimo Schachfreund, lo publicó en 1848 en la revista especializada Berliner Schachzeitung. Puesto que la dama puede desplazarse horizontal, vertical o diagonalmente, el problema equivale a situar ocho fichas en el tablero de forma que no haya dos en la misma fila, columna o diagonal (lo cual lo emparenta con el popular sudoku).

El problema de las ocho damas fue analizado, entre otros, por el mismísimo Gauss, que halló 76 de las 92 soluciones posibles; pero el primero en encontrarlas todas, en 1850, fue un amigo suyo, el matemático ciego Franz Nauck.

En realidad, solo hay 12 soluciones básicas, y las 80 restantes se obtienen por giros y simetrías; 11 de las soluciones básicas valen por 8: girando cualquiera de ellas 90º, 180º y 270º se obtienen tres más, y las cuatro dan lugar a otras cuatro por simetría especular; pero la duodécima (damas en a3, b5, c2, d8, e1, f7, g4 y h6) solo vale por cuatro, pues tiene simetría central. Las 12 soluciones básicas dan, pues, lugar a 11 x 8 + 4 = 92 soluciones distintas.

Puesto que solo puede haber una dama por columna, podemos expresar numéricamente las soluciones anotando, de izquierda a derecha, los números de las filas que ocupan. Así, la solución simétrica que acabamos de ver sería 35281746. El problema de las ocho damas se puede convertir, de este modo, en un problema aritmético, que consiste en tomar, de entre todas las permutaciones de los dígitos del 1 al 8, las que cumplen cierta condición. Sin embargo, esta notación numérica no es de gran ayuda, salvo para realizar un programa de búsqueda por ordenador, pues las permutaciones de los ocho dígitos son 8! = 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 40.320, entre las cuales hay que buscar las 92 que cumplen la condición requerida. Por cierto, ¿qué condición es esa?

Más difícil todavía, ¿hay alguna solución en la que no haya ningún grupo de tres damas alineadas? ¿Cuál es -si existe- su notación numérica?

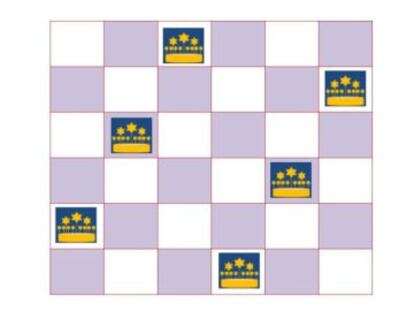
Solo hay una solución básica para el tablero de 4 x 4 y otra para el de 6 x 6, y dos para el de 5 x 5, que en la notación numérica antes establecida serían, respectivamente, 2413, 246135, 25314 y 35241; las tres primeras tienen simetría central.

Problemas afines

¿Cuántas damas son necesarias, como mínimo, para cubrir todo el tablero? Por cubrir o abarcar el tablero se entiende que todas las casillas estén a tiro de alguna de las damas.

¿Y para abarcar tableros de 9 x 9, 10 x 10 y 11 x 11?

¿Cuántas torres podemos colocar en el tablero de forma que ninguna amenace a ninguna otra? ¿De cuántas maneras distintas podemos colocarlas?

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’