Desafío criptográfico: el código secreto del Cofre de los Deseos

Siglos atrás, la Tierra Tercia estaba dividida en cinco reinos, Reino 1, Reino 2, Reino 3, Reino 4 y Reino 5. Las fronteras entre sus territorios se cruzaban en el Pico Cúbico, dentro del Bosque Mágico, cuidado por el Mago del Bosque. Tras muchos años de guerras constantes entre los reinos, siguió al fin un largo periodo de paz, en el que Mago del Bosque creó una pócima mágica que concedía al que la probase cualquier deseo. Para salvaguardar tan peligroso poder, introdujo la pócima dentro de un cofre, que cerró con un candado numérico que sólo se abría introduciendo un número secreto. Después, convocó a los líderes de los cinco reinos, y les habló así:

“Dentro de este cofre he depositado una pócima que concederá un deseo a quien beba de ella. Para abrir el cofre es necesario conocer un número secreto, del que ahora os daré un fragmento a cada uno. Cada vez que alguien beba, vendré para cambiar el número secreto y repartiros nuevos fragmentos.

Es mi deseo que colaboréis; pues es necesario combinar al menos dos fragmentos para encontrar el número secreto:

Mira, amigo, tenemos al frente un cruce de caminos

Uno vertical, de arriba a abajo

Otro horizontal, de izquierda a derecha

Su cruce es un doble cero.

Partamos desde tu punto hasta el mío,

encontrémonos en el camino vertical,

y pensemos cuán lejos está el cruce; dicha distancia este cofre abrirá

Y así entregó a cada reino un fragmento, que no era sino una pareja de números: al Reino 1 le correspondió el fragmento (1,4), al Reino 2 el (2,1), al Reino 3 el (3,-2), al Reino 4 el (4,-5) y al Reino 5 el (5,-8).

En varios meses no se abrió el Cofre de los Deseos. Durante este tiempo, más de un líder, arrastrado por el ansia de un deseo determinado, intentó taimadamente obtener por sí solo el secreto a partir de su fragmento… pero sin éxito. Llegó sin embargo el día aciago en el que coincidieron en el Reino 2 y el Reino 5, dos malvados líderes. Ambos enviaron al Pico Cúbico a sendos expertos en matemáticas, que encontraron rápidamente la manera de calcular el número secreto: los fragmentos eran puntos del plano XY, que, por supuesto, definían una única recta. En el caso de los dos reinos allí presentes, los fragmentos (2,1) y (5,-8) determinaban la recta y = -3x + 7. Esa recta “secreta” cortaba el eje de ordenadas (el camino vertical, el eje OY, en el que las x valen 0) en el punto (0,7). Por tanto, razonaron, el número secreto que abriría el cofre era el 7, pues 7 era la distancia del punto de la recta secreta con el origen, que no era otro que el punto (0,0).

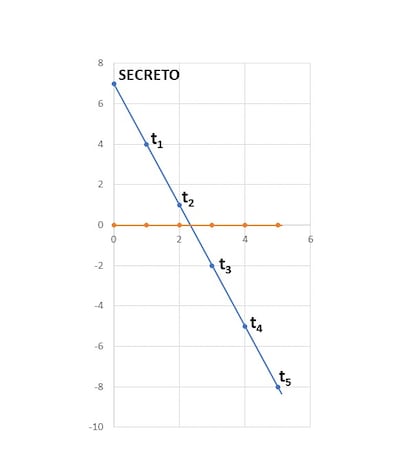
En efecto, probaron con el número 7 y el candado se abrió. El líder del Reino 2 bebió un trago de la poción y pidió quedarse con la cosecha del Reino 3.

Apareció entonces el Mago del Bosque para cerrar el cofre con la pócima en su interior y cambiar el número secreto del candado. Tras ello, entregó a los líderes los nuevos fragmentos: al Reino 1 el fragmento (1,15), al Reino 2 el (2,17), al Reino 3 el (3,19), al Reino 4 el (4,21) y al Reino 5 el (5,23).

Los líderes de los Reinos 1, 3 y 4 se movieron rápidamente y acordaron hacer uso del Cofre de los Deseos antes de que lo volviesen a hacer los malintencionados Reinos 2 y 5. Juntando los fragmentos del Reino 1 y el Reino 3, encontraron el número secreto y pidieron que el cofre nunca más pudiera abrirse de nuevo por una coalición de los Reinos 2 y 5.

Apareció al instante el Mago del Bosque, convocó a los líderes de los cinco reinos y les habló así: “A partir de hoy necesitaréis combinar al menos tres fragmentos para encontrar el número secreto y poder así abrir el Cofre de los Deseos”.

Y entregó al Reino 1 el fragmento (1,22), al Reino 2 el (2,29), al Reino 3 el (3,32), al Reino 4 el (4,31) y al Reino 5 el (5,26).

Pasado el tiempo, los Reinos 2 y 5 derrocaron a sus malvados gobernantes. Los líderes de los Reinos 1, 3 y 4, pensando en establecer una alianza global, decidieron subir una vez más al Pico Cúbico y pedir al Cofre de los Deseos que en adelante, hiciese falta combinar los cinco fragmentos de los cinco reinos para abrir el cofre.

¿Cuál fue el número secreto usado por los reinos 1 y 3 para abrir el cofre y pedir que los malvados líderes de los reinos 2 y 5 no pudieran hacerlo más? ¿Qué número secreto usarían los tres reinos cooperantes en la última ocasión para abrir el Cofre de los Deseos? ¿Cómo se las arreglará ahora el Mago del Bosque para que sean necesarios cinco fragmentos para abrir el cofre?

Los desafíos criptográficos se publicarán cada 15 días (aunque en esta última entrega nos hemos retrasado, pedimos disculpas ;-) ). Los lectores pueden dejar sus soluciones y debatir sobre el problema en los comentarios de esta página, por lo que se recomienda a quien quiera resolverlo por sí mismo no leerlos hasta haber descifrado el enigma. También pueden enviar sus respuestas al correo desafioscriptograficos@gmail.com. En cada nuevo desafío publicaremos la solución del anterior, acompañada de un comentario con algunas ideas originales o inspiradoras que hayamos recibido.

Javier Herranz es investigador del grupo MAK y profesor de Matemáticas Aplicadas en la Universitat Politècnica de Catalunya.

SOLUCIÓN AL DESAFÍO ANTERIOR

El anterior desafío trataba sobre la criptografía visual, un área iniciada por el israelí Adi Shamir (la S del criptosistema RSA) en 1994.

La respuesta a la primera pregunta ―qué mensaje se obtiene al superponer la primera transparencia con la segunda que se ha propuesto― es que en vez de una A en blanco con fondo negro, se obtiene una L negra en fondo blanco. En realidad a partir de una transparencia dada se podría obtener cualquier imagen (que tenga la misma calidad de definición) utilizando una segunda transparencia apropiada.

En el segundo ejercicio, la imagen recuperada si se juntan las transparencias 1 y 4 o 2 y 3 es:

Nuestros lectores, como (los ya habituales) Joaquín y Javier, han llegado a la solución sin usar el “mecanismo analógico” sugerido en el texto, utilizando diferente código para combinar y luego depurar las imágenes.

Por otro lado, algo similar a lo planteado con imágenes en este desafío podría hacerse con sonido (como nos planteaba Ramiro por correo, y Salva Fuster desde la sección de comentarios). De hecho, reproducimos aquí su reto musical, por si aún alguien se anima a resolverlo:

Una palabra ineludible con un pequeño toque musical (en ocasiones disonante) a dos voces:

A: GDBAB - DBDGD - BABDB - DGECB - CECEG - ECBCE - CEGFC - BCFCF - GFCBC - FCFGG - BABGB

B: FEEBA - EEGFG - ABEGE - ECAFE - FFBAF - FBCBF - BFFGF - EBBBB - FGFCB - GFBFC - ABAAA

- ¿Qué melodía actúa como clave (hay que tener en cuenta que en la clave, las F realmente son F#)?

- ¿Cuál es la palabra oculta?

- ¿Cuál es el sistema que permite cifrar/descifrar el mensaje?

Un método acústico se describe también en el artículo Audio and Optical Cryptography, propuesto por Desmedt et al., en el congreso ASIACRYPT 98. El lector dispone además una demo on-line asociada al esquema descrito en ese artículo en este enlace: https://crypto.cs.jmu.edu/visualaudiocrypto/AudioCryptography.htm

Bibliografía:

-101 computing: https://www.101computing.net/visual-cryptography/

-Douglas R. Stinson: An Explication of Secret Sharing Schemes. Des. Codes Cryptogr. 2(4): 357-390 (1992)

-Paolo D’Arco, Roberto De Prisco: Visual Cryptography - Models, Issues, Applications and New Directions. SECITC 2016: 20-39

-Giuseppe Ateniese, Carlo Blundo, Alfredo De Santis, Douglas R. Stinson: Visual Cryptography for General Access Structures. Inf. Comput. 129(2): 86-106 (1996)

-Moni Naor, Adi Shamir: Visual Cryptography. EUROCRYPT 1994: 1-12

Puedes seguir a EL PAÍS TECNOLOGÍA en Facebook y Twitter o apuntarte aquí para recibir nuestra newsletter semanal.