Así se están moviendo las encuestas en Cataluña

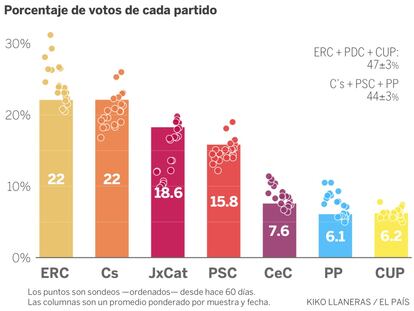
Quedan diez días para las elecciones catalanas y las encuestas no paran de moverse. El promedio de sondeos coloca a ERC y Ciudadanos muy igualados. Los dos rondan el 22% de los votos y les siguen Junts per Catalunya (18,6%), PSC (16%), CeC-Podem (7,6%), PP (6%) y la CUP (6%).

El gráfico siguiente muestra la evolución de los sondeos desde octubre hasta este lunes. ERC ha caído del 28% al 22%, mientras JxCat subía del 10% al 18%. El cambio se produjo a principios de noviembre, cuando se confirmó que Carles Puigdemont sería el candidato de JxCat. También se han movido las otras formaciones. El PSC y Ciudadanos han subido tres y cuatro puntos, mientras menguaban los apoyos del PP y los comunes. El PP sufren fugas en favor de Ciudadanos y el partido de Xavier Domènech en varias direcciones.

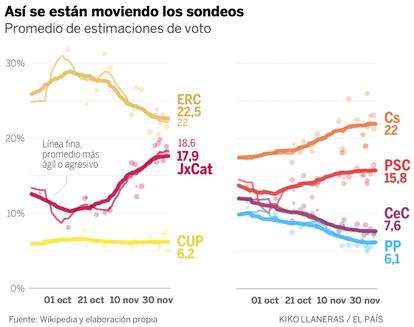
Estos movimientos plantean un dilema técnico al hacer el promedio. El típico del filtrado de señales: si confiamos demasiado en las encuestas recientes, introducimos ruido; pero si damos demasiado peso a las encuestas antiguas, veremos los cambios con retraso. Para mostrar esa diferencia, en el gráfico anterior he representado un promedio cauto (línea gruesa) y otro agresivo (línea fina). Con el promedio cauto, ERC se mantiene en el 22,5% de los votos —todavía por encima de Cs— y JxCat se queda en el 17,9%. No hay forma de decidir cuál de los promedios es mejor y por eso ofrecemos los dos.

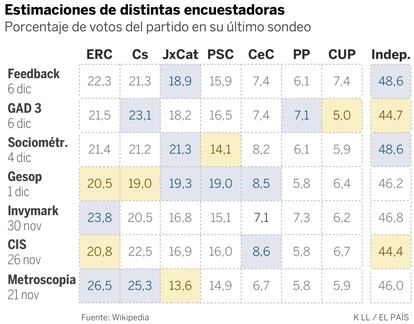
Otro motivo de incertidumbre al analizar los sondeos son las diferencias entre encuestadoras. Feedback, por ejemplo, todavía coloca a ERC primero (con tres puntos de ventaja sobre JxCat y uno sobre Cs). En cambio, Gesop y Sociométrica igualan a los tres partidos de arriba, y GAD3 cree que el más votado será Ciudadanos. Estas diferencias son habituales y sirven para recordarnos que los sondeos nunca son absolutamente precisos. Lo normal es que cometan errores de dos o tres puntos con algún partido y no es raro que se desvíen más.

El partido más votado

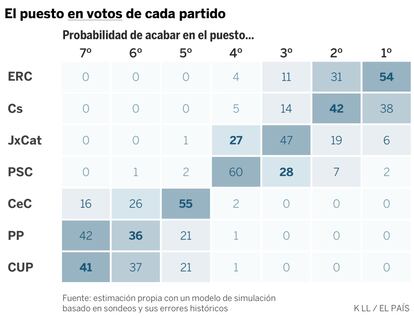
Teniendo en cuenta todas estas encuestas, ¿qué probabilidad tiene cada partido de acabar siendo el más votado? Para responder esa pregunta he hecho 10.000 simulaciones a partir del promedio de votos (cauto). Utilizo el modelo que presentamos hace unos días, que agrega los sondeos y ha sido calibrado con la precisión histórica de miles de encuestas.

La igualdad en votos es evidente. ERC tiene un 54% de probabilidades de ser el más votado, pero puede ser el segundo (31%) o el tercero (11%). Ciudadanos tiene un 38% de probabilidades de ser primero y un 42% de ser segundo. Tampoco serían una enorme sorpresa si acaba siendo tercero: es lo que ocurre en el 14% de las simulaciones (una de cada siete). También he calculado probabilidades dos a dos: JxCat tiene un 15% de opciones de superar a ERC en votos, y el PSC un 10% de superar a Ciudadanos.

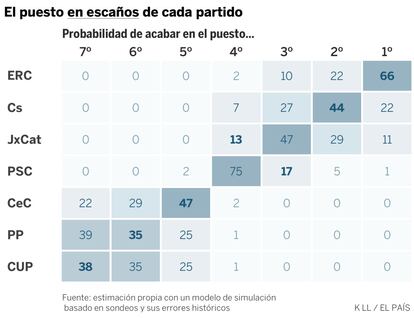
En escaños la ventaja de ERC es más clara. La razón es que ERC y JxCat consiguen más votos fuera de la provincia de Barcelona y el sistema electoral hace que esos votos se traduzcan en más escaños. En el 66% de las simulaciones ERC es el partido con más escaños, en el 22% es Ciudadanos, y en el 11%, JxCat. Las opciones de Cs para superar en escaños a ERC caen al 24%.

Además, en este caso son posibles los empates. En un 5% de las simulaciones, ERC y Cs suman los mismos escaños, y en el 3% lo hacen ERC y JxCat. Podría incluso darse un triple empate, pero no es fácil: sólo pasa una de cada 500 veces.

Metodología del modelo. Las predicciones las produce un modelo estadístico basado en sondeos y en su precisión histórica. El modelo es similar al que usamos en Francia y Reino Unido. Funciona en cuatro pasos: 1) agregar y promediar las encuestas en Cataluña, 2) proyectar ese promedio sobre cada provincia, 3) incorporar la incertidumbre esperada, y 4) simular 10.000 elecciones para calcular probabilidades.

Paso 1. Promediar las encuestas. El modelo agrega las estimaciones de voto de docenas de sondeos. La mayoría pueden consultarse en Wikipedia. Hay dos razones para hacer este promedio: sirve para reducir el error de muestreo y además ofrece una «cocina» de consenso. El promedio está ponderado para tener en cuenta el tamaño de muestra, la empresa encuestadora y la fecha del sondeo.

Nota. Los promedios están ponderados por fecha según una ley exponencial decreciente. El promedio cauto define esa ley con una vida medida de 10 días (las encuestas de hace 10 días tienen la mitad de peso) y el promedio agresivo utiliza una de 5 días. Además, el promedio cauto ignora las encuestas con más de 25 días y el agresivo las de hace 15 días.

Paso 2. Proyectar el promedio a cada provincia. Antes de calcular los escaños es necesario estimar el porcentaje de votos de cada partido en cada provincia. Para eso hacemos una proyección lineal del promedio de votos en todo Cataluña. La proyección tiene en cuenta resultados históricos en cada provincia (del 26J y el 27S) y los últimos sondeos del CIS y del CEO.

Paso 3. Incorporar la incertidumbre de las encuestas. Este paso es el más complicado. También es el más importante. Para predecir el resultado «más probable» basta usar el promedio de votos y estimar los escaños. Pero si queremos saber qué probabilidad tienen distintos resultados necesitamos algo más: un modelo probabilístico. Necesitamos estimar la precisión esperada para los sondeos en Cataluña. ¿De qué magnitud son los errores habituales? ¿Cómo de probable es que se produzcan errores de 1, 2 o 5 puntos? Para responder esas preguntas hemos analizado el error de miles de encuestas.

Calibrar los errores esperados. Primero he estimado el error de las encuestas en España. He construido una base de datos con encuestas de 23 elecciones desde 1982 —incluyendo todas las generales y una docena de elecciones recientes. El error absoluto medio (MAE) de los promedios de encuestas en España ha rondado los 2,1 puntos por partido. Pero esos errores dependen al menos de dos cosas: del tamaño del partido y de la cercanía de las elecciones. Para tener en cuenta esos dos factores hemos recurrido a la base de datos de Jennings y Christopher Wlezien. Hemos analizado los errores de más de 2.700 encuestas en 198 elecciones de 19 países occidentales. Así hemos construido un modelo sencillo que estima el error MAE del promedio de votos estimado por las encuestas para cada partido, teniendo en cuenta: i) su tamaño (es más fácil estimar un partido que ronda el 5% en votos que uno que supera el 30%), y ii) los días que faltan hasta las elecciones (porque las encuestas mejoran al final).

Distribución. Para incorporar la incertidumbre al voto de cada partido en cada simulación utilizo varias distribuciones multivariables. Uso distribuciones t-student en lugar de normales para que tengan colas más largas (curtosis): eso hace más probable que sucedan eventos muy extremos. Las ventajas de esa hipótesis la explica Nate Silver. El nivel de curtosis lo he estimado con la base de datos. Luego defino la matriz de covarianzas de estas distribuciones para que i) la suma de los votos no sobrepase el 100% (unaidea de Chris Hanretty), y ii) consideren correlaciones entre partidos cercanos (por ejemplo, ERC y JxCat). Esas correlaciones las he basado en las matrices de transferencias del CIS y de Metroscopia. La incertidumbre la incorporo con cinco distribuciones, una a nivel catalán y otra en cada provincia. La primera distribución introduce errores iguales para el voto de un partido en toda Cataluña. Es importante hacerlo así porque en general los errores de las encuestas son sistémicos e iguales en todos los territorios. Si los asumimos independientes, los errores se cancelan entre provincias y el modelo falla por exceso de confianza. Esto pasó con algunos modelos de las elecciones de EE UU en 2016. La segunda parte de la incertidumbre la incorporo sobre cada provincia. Por último, hay que escalar la amplitud de las matrices de covarianza para que las distribuciones de voto que resultan al final tengan el MAE y la desviación estándar esperados según la calibración.

Paso 4. Simular. El último paso consiste en ejecutar el modelo 10.000 veces. Cada iteración es una simulación de las elecciones con porcentajes de voto que varían según las distribuciones definidas en el paso anterior. Los resultados en esas simulaciones permiten calcular las probabilidades de que haya una mayoría de ciertos partidos, de que un candidato logre cierto número de votos, quede primero, etc.

Por qué encuestas. El modelo se basa por entero en encuestas. Existe la percepción de que los sondeos no son fiables, pero lo cierto es que a nivel nacional fallaron por pocos puntos incluso con Trump y con el Brexit. En otras elecciones recientes, como las francesas, las holandesas o las de País Vasco y Galicia, los sondeos dieron poco que hablar porque estuvieron acertados. Las encuestas raramente son perfectas, pero son capaces de predecir elecciones en términos probabilísticas. Además,no existe una alternativa que haya demostrado mayor capacidad de predicción.