Matemáticas para proteger la democracia

La democracia es considerada el sistema político que más voz y poder otorga a los ciudadanos. En palabras del premio Nobel Octavio Paz, “sin democracia, la libertad es una quimera”. Sin embargo, a veces esa herramienta puede verse manipulada sin que la ciudadanía se dé cuenta. Esto es lo que ocurre a veces con una técnica política conocida como gerrymandering. Pero las matemáticas permiten detectarlo.

En las elecciones legislativas de Estados Unidos, como las que tuvieron lugar el pasado 6 de noviembre, cada estado se divide en tantos distritos electorales como miembros para la Cámara de Representantes le sean asignados, y cada distrito elige como representante al candidato que obtiene la mayoría de votos. Cada diez años, el gobierno de un estado puede modificar a su antojo el diseño de esas circunscripciones electorales: esta es la táctica del gerrymandering. "Hay casos en los que se ha utilizado para propiciar avances sociales y garantizar la representatividad de minorías raciales, pero su intención habitual es obtener beneficios políticos", indica Carmen Méndez, coordinadora del máster de Estudios Americanos de la Universidad Complutense de Madrid.

Aunque el término gerrymandering se inventó en EE. UU., el fenómeno también “puede darse de forma excepcional en otros países como Francia e Italia”, indica Méndez. Sin embargo, en España no: “Las fronteras de los distritos electorales están basadas en un diseño provincial de la Constitución de 1978 y no se pueden modificar para las elecciones generales ni para otras votaciones”.

En los países en los que se aplica, esta estrategia puede cambiar considerablemente el resultado. Imaginemos un estado compuesto por 25 personas que debe elegir a cinco representantes entre dos partidos: el verde y el azul. El 60 % de la población vota al verde y, el 40 %, al azul. En la primera imagen, el trazo de los cinco distritos electorales hace que el partido verde obtenga tres representantes y el partido azul dos, siendo el número de representantes de cada partido proporcional al voto. Sin embargo, en el segundo diseño el partido verde se lleva los cinco representantes y en el tercer ejemplo solo dos, a pesar de tener la mayoría. “El partido en el poder puede beneficiarse del rediseño de las fronteras electorales y conseguir que el voto se concentre a su favor. Los otros partidos y sus votantes salen perjudicados”, explica Méndez.

En situaciones reales es complicado determinar si esta estrategia se ha utilizado de forma fraudulenta. En el ejemplo anterior se observa que el trazado no tiene ni siquiera por qué tener una forma sospechosa para favorecer a un partido (como sucede en el segundo gráfico). ¿Cómo saberlo entonces? El grupo de matemáticos Quantifying Gerrymandering de la Universidad de Duke (EE. UU.) ha desarrollado técnicas que intentan proteger la democracia. “Utilizando algoritmos de muestreo estadístico, simulamos miles de posibles mapas con diferentes dibujos de distritos que cumplen criterios de distribución neutrales, teniendo en cuenta la geografía y las opiniones políticas”, explica el investigador principal del proyecto, Jonathan Mattingly. Concretamente, “usamos los llamados métodos de Monte Carlo basados en cadenas de Markov, que fueron desarrollados como parte del proyecto Manhattan”, detalla el también investigador del grupo Gregory Herschlag.

Aplicando a estos mapas las votaciones históricas a lo largo de los años, obtienen un rango típico de resultados electorales que pueden usar para comparar cualquier otro mapa. “Si un cierto diseño se encuentra en un extremo atípico del conjunto, podemos concluir que se trata de manipulación partidista”, aclara Herschlag.

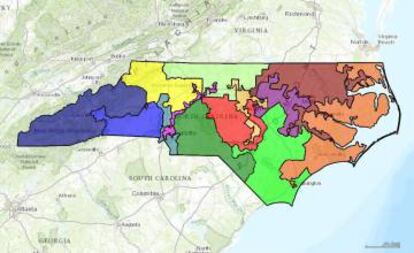
Precisamente, el grupo se encontró con que “los mapas de distritos de Carolina del Norte de las elecciones legislativas de 2012 y 2016 tenían dentro de nuestra distribución valores estadísticos altamente atípicos”, indica Mattingly. El Partido Demócrata obtuvo, respectivamente, cuatro y tres de los 13 representantes totales, “un resultado que solo se daba en menos del 1% de los mapas simulados”. También había características sospechosas, como distritos sobrecargados de votantes demócratas y lo contrario. “Simplemente cambiando el trazado, los demócratas podían pasar a tener nueve representantes; la elección variaba enormemente sin modificar ni un solo voto”, añade el matemático. En los comicios de este año, el resultado ha vuelto a ser tres contra diez.

El descubrimiento llevó a Mattingly a testificar como experto ante el tribunal de Carolina del Norte en el Common Cause v. Rucho. “Los jueces concluyeron que el caso era extremo e inconstitucional. Ahora está por ver si la Corte Suprema de los Estados Unidos comparte este punto de vista”, explica Mattingly.

Méndez afirma que los modelos matemáticos facilitan determinar si esta práctica debería ser legal o no, "ya que en el terreno político en ocasiones se utiliza una retórica conectada con lo emocional y los derechos individuales, que dificulta una visión de conjunto". Los investigadores de Duke lo tienen claro: “Las matemáticas pueden ayudar a terminar con el gerrymandering porque solo una comprensión profunda del problema puede hacerlo”. 

Juan José Marín es investigador del ICMAT. Patricia Ruiz Guevara es matemática por la Universidad de Murcia y periodista científica.

Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: "Un matemático es una máquina que transforma café en teoremas".