El triángulo de Reuleaux

Si, dado un triángulo equilátero, trazamos sendos círculos con centros en los tres vértices y radio igual al lado del triángulo, la intersección de dichos círculos es un triángulo de Reuleaux, denominado así en honor del ingeniero alemán Franz Reuleaux (1829-1905), considerado el padre de la cinemática. (¿Puedes calcular su área, si tomamos como unidad el lado del triángulo equilátero?).

El triángulo de Reuleaux es la figura de anchura constante más simple después, obviamente, del círculo. Y, como señala AlienJ Campo en respuesta a la pregunta de la semana pasada: “Otras formas para alcantarillas que impidiesen la caída por el hueco puede ser el triángulo de Reuleaux u otros polígonos del mismo tipo, aunque serían menos prácticas tanto para la construcción como para el cierre del agujero, porque no girarían sobre el borde del soporte con la misma facilidad”.

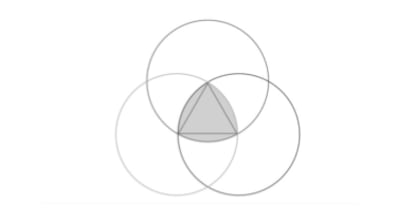
Una figura de anchura constante es aquella que, si la encerramos entre dos rectas paralelas tangentes a ella, la distancia entre dichas paralelas siempre es la misma, independiente de la posición de la figura.

El triángulo de Reuleaux, aunque su estudio cinemático y sus aplicaciones mecánicas se deben al ingeniero que le dio nombre, es conocido desde antiguo. Leonardo da Vinci lo utilizó en su proyección en octantes (pero ese es otro artículo), y lo encontramos en las ventanas góticas de algunas iglesias, incluida la Sagrada Familia.

Con cualquier polígono regular de un número impar de lados podemos llevar a cabo una construcción similar a la del triángulo de Reuleaux trazando desde cada vértice una circunferencia que pase por los dos vértices del lado opuesto. Obtenemos así los distintos polígonos de Reuleaux, también de anchura constante y, por ende, candidatos a tapas de alcantarilla. Y no solo a tapas: hay incluso bicicletas cuyas ruedas son polígonos de Reuleaux (¿se te ocurre cuáles pueden ser sus ventajas sobre las ruedas circulares?).

¿Por qué no hay polígonos regulares de Reuleaux con un número par de lados? ¿O sí que los hay? ¿Se pueden obtener figuras de anchura constante a partir de polígonos irregulares?

En cuanto a las posibles formas de las espadas envainables, además de la espada de hoja recta y el sable cuya curvatura es un arco de circunferencia, también se podría envainar una espada helicoidal; pero no parece que esta espada-sacacorchos pudiera resultar muy práctica.

El pico del ánfora

La peculiar forma de las ánforas romanas ha suscitado un amplio debate entre mis amables lectoras/es, sobre todo por su remate en punta, que a primera vista parece poco práctico. Sin embargo, ese pico macizo y muy sólido permitía manejar las ánforas con cierta brusquedad. Era un tope resistente al apoyarlas en el suelo, e incluso se podía arrastrarlas sin gran esfuerzo y sin miedo a que se rompieran (es impresionante el enorme número de ánforas romanas que han llegado enteras hasta nuestros días). Además, el pico era como una tercer asa a la hora de levantarlas para verter su contenido. Y, last but not least, al almacenar las ánforas en la bodega de una nave, que era su medio de transporte habitual, los picos de una hilera se encajaban entre los cuellos y las asas de otra hilera, con lo que se conseguía una estiba compacta y estable.