Sin líneas de fractura

El famoso número de Ramanujan, como vimos la semana pasada, es el menor que puede expresarse de dos maneras distintas como suma de dos cubos: 1729 = 12³ + 1³ = 10³ + 9³; pero solo si especificamos que estamos hablando de números naturales, es decir, enteros y positivos, pues si también tenemos en cuenta los enteros negativos hay infinitos menores que 1729 que cumplen la condición (sin ir más lejos, –1729).

Por otra parte, la afirmación de Hardy de que el número era poco interesante entraña en sí misma una paradoja, señalada en su día por el maestro Martin Gardner, independientemente de la propiedad observada por Ramanujan. ¿Qué paradoja?

La relación cuantitativa entre los poliominós y los esquemas de Young no ha suscitado comentarios entre los lectores, por lo que la cuestión queda pendiente.

Mosaicos de poliominós

Y hablando de Martin Gardner y de poliominós, recordemos que, aunque fue Solomon W. Golomb quien los “bautizó” a mediados del siglo pasado, fue Gardner quien los popularizó en su sección de juegos matemáticos de Scientific American, y que uno de los problemas que planteó fue el de las líneas de fractura. Por ejemplo, en la figura vemos un rectángulo de 5x12, formado por cinco pentominós, en el que no hay ninguna línea de fractura, es decir, ninguna recta horizontal o vertical que vaya de lado a lado, y que en el caso de tratarse de una construcción física representaría una debilidad estructural.

En los dos tatamis siguientes, sin embargo, tanto en el de 4x4 como en el de 6x6, hay dos líneas de fractura verticales.

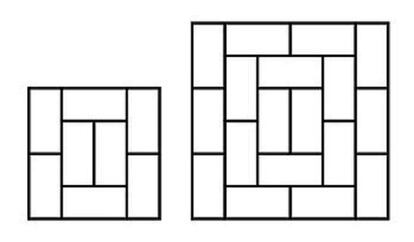
¿Podrían reordenarse sus piezas de manera que no hubiese tales líneas de fractura? Y en el caso de que no sea posible, ¿cómo se puede demostrar tal imposibilidad?

En el caso del tatami de 4x4, la imposibilidad se hace evidente tras unos cuantos intentos, pero en el de 6x6 no es tan obvia, y el propio Golomb dio una elegante demostración que invito a mis sagaces lectores a intentar emular (o mejorar, llegado el caso). Cabe preguntarse, dada la imposibilidad en el caso de 6x6, cuál es el rectángulo de mínimo tamaño y sin líneas de fractura que puede formarse con dominós. Y una vez hallado este rectángulo mínimo, ¿podemos usarlo como punto de partida para, añadiéndole los dominós necesarios, formar un cuadrado de 8x8 (es decir, un recubrimiento del tablero de ajedrez) sin líneas de fractura?

Evidentemente, para que un rectángulo pueda ser recubierto por dominós, su área (tomando como unidad el lado menor de un dominó) ha de ser par, y para que pueda recubrirse sin líneas de fractura sus dos lados han de ser mayores de 4. Se puede demostrar (¿cómo?) que todos los rectángulos y cuadrados que cumplen ambos requisitos pueden ser recubiertos con dominós sin líneas de fractura, con la única y notable excepción del cuadrado de 6x6.

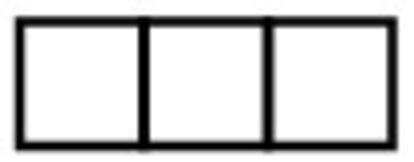
A partir de estas consideraciones, quienquiera que posea un juego de fichas de dominó podrá darle un nuevo e instructivo uso. Y quien se atreva a ir un paso más allá puede experimentar con los trominós, intentado descubrir, por ejemplo, cuál es el rectángulo mínimo que puede recubrirse con trominós rectos (o sea, rectángulos de 1x3) sin líneas de fractura.

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal