Matemáticas para crear un mapa celular de las enfermedades

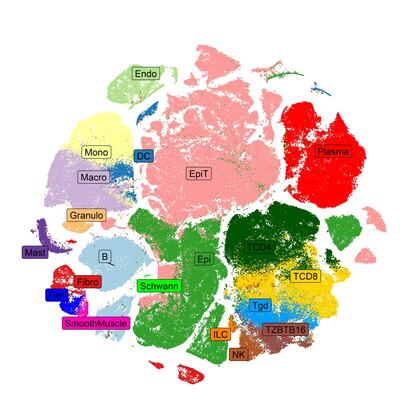
Se estima que el cuerpo humano contiene 30 billones de células organizadas en tejidos. Cada célula humana contiene 6.400 millones de nucleótidos de ADN, que se estructuran en unos 20.000 genes codificantes y cada gen puede dar lugar a múltiples proteínas. Un consorcio internacional de científicos está tratando de componer un atlas (Human Cell Atlas) para caracterizar molecular (ADN, genes, proteínas) y morfológicamente todas las células que componen el cuerpo humano. Este tremendo esfuerzo técnico y económico tiene que incorporar métodos matemáticos que permitan extraer toda la información relevante y a la vez simplificarla, para hacerla interpretable. Para hacer frente a este reto, en los últimos años se han popularizado las técnicas de reducción de la dimensionalidad para el análisis de datos de célula única.

Actualmente podemos caracterizar cada célula de manera muy exhaustiva. Por un lado, gracias a complejas técnicas de biología molecular, podemos identificar las mutaciones presentes en el ADN de una célula concreta o cuantificar la expresión del catálogo de genes y proteínas específicamente expresados en ella. Esta información se incorpora en una matriz con más de 20.000 filas —el número aproximado de genes expresados en un experimento—, y tantas columnas como células se estén analizando, actualmente decenas de miles. Por otro lado, técnicas de imagen —con cada vez más resolución— se utilizan para explorar los cambios de forma, tamaño o estructura de cada célula.

Nuestra capacidad para estudiar esta gran cantidad de datos generados conjuntamente es muy limitada, debido tanto a su dimensionalidad como a su heterogeneidad. Las técnicas de reducción de la dimensionalidad permiten crear mapas celulares en tan sólo dos dimensiones, escogidas para garantizar que se preserva la mayor cantidad de información posible a la vez que se sintetiza, facilitando la identificación de grupos de células similares o clústers, su visualización y su posterior interpretación. Gracias a estos mapas se han podido identificar y cuantificar nuevos subtipos celulares asociados con la génesis y el desarrollo de distintas enfermedades complejas, desde el cáncer a las enfermedades cardiovasculares.

Las técnicas más tradicionales de reducción de la dimensionalidad, como el análisis de componentes principales propuesto por Karl Pearson hace ya más de un siglo, se basan en la proyección lineal de la información en un hiperplano, como una fotografía proyecta el mundo tridimensional en el plano de foco. Estas técnicas tienen la ventaja de respetar relativamente bien las distancias reales en el espacio de dimensiones reducidas, pero a menudo son incapaces de capturar toda la complejidad contenida en los datos, sobre todo si la relación entre las variables del sistema es no lineal, como sucede con las variables moleculares y fenotípicas que se pueden medir en una célula.

Por ello, en la última década se han propuesto nuevas técnicas de reducción de la dimensionalidad no lineales. La idea tras ellas es identificar un nuevo espacio en dos dimensiones que resuma la mayor cantidad de información posible, preservando las distancias locamente, en detrimento de perder, en cierta medida, la estructura global. Esto permite que podamos identificar grupos de elementos similares, por ejemplo, células, en la representación bidimensional, aunque las distancias entre los distintos grupos estén distorsionadas.

Su comportamiento es similar al de la proyección cartográfica de Mercator, la más utilizada para realizar mapas mundiales, que aumenta la distorsión de áreas y distancias a medida que nos acercamos a los polos. A nivel local las distancias se mantienen, es decir, zonas cercanas geográficamente lo están en un mapa, pero zonas alejadas no mantienen las distancias cuando atraviesan meridianos, lo cual no impide que el mapa siga siendo útil.

Para lograr su objetivo, estos nuevos métodos utilizan algoritmos iterativos basados en grafos dirigidos, construidos a partir del cálculo de distancias entre vecindades de datos, generando fuerzas atractoras o repulsivas en el nuevo espacio de representación dependiendo de su similitud. El modo en que se define el concepto de vecindad en cada dato, junto con cómo y en qué circunstancias se generan estas fuerzas, es la clave y la principal diferencia entre los distintos algoritmos que podemos encontrar, como t-distributed stochastic neighbor embedding (t-sne) o el más reciente Uniform Manifold Approximation and Projection (UMAP).

La teoría matemática detrás de este último mezcla conceptos de topología algebraica, geometría riemaniana y lógica difusa para generar una representación de los datos en forma de grafo; y la teoría de probabilidades, optimización y programación matemática para optimizar su representación lo más fielmente posible en un espacio de dimensiones menores. El resultado es un método de reducción de dimensionalidad potente, rápido y escalable, de gran utilidad en el análisis de datos multidimensionales y, en particular, en el análisis de datos moleculares de célula única. Pese a sus fortalezas, es crucial entender las matemáticas subyacentes para interpretar sus resultados de manera correcta.

Estos nuevos algoritmos de reducción de la dimensionalidad representan bien el tipo de metodologías que debemos seguir desarrollando para poder analizar las grandes cantidades de datos biomédicos que se están generando, cuyo volumen y complejidad seguirá aumentando en las próximas décadas. Sólo con las matemáticas adecuadas podremos seguir avanzando en el entendimiento de los mecanismos causales de las enfermedades complejas, del cáncer al Alzheimer y a las enfermedades cardiovasculares y así, en la implementación de la medicina de precisión.

Fátima Sánchez Cabo es directora de la Unidad de Bioinformática del Centro Nacional de Investigaciones Cardiovasculares (CNIC) y profesora asociada de la Universidad Autónoma de Madrid;

Daniel Jiménez Carretero es técnico senior de la Unidad de Bioinformática del CNIC.

Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.

Edición y coordinación: Ágata A. Timón G Longoria (ICMAT).

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.