Matemáticas para describir las olas del mar
Los matemáticos buscan, desde hace siglos, soluciones a las ecuaciones que se correspondan con olas tubo, las favoritas de los surfistas

Desde el siglo XVIII, los matemáticos han propuesto diversos modelos para describir las olas de superficie, que se propagan en la interfase entre dos medios diferentes. En concreto, las investigaciones buscan determinar las condiciones que garantizan la existencia de estas olas y estudiar la forma y propiedades de las mismas.
Los modelos capturan el movimiento de una masa de agua bajo un cuerpo de aire, empleando un conjunto de ecuaciones en derivadas parciales, las llamadas ecuaciones de Euler. Estas ecuaciones se deducen al aplicar leyes de conservación a la masa de agua: la conservación del volumen y la conservación del momento. Además, se imponen diferentes condiciones a la interfase: se puede considerar la presencia de la gravedad y también la tensión superficial, es decir, la tensión mecánica de cohesión de las partículas en la interfase, que provoca que objetos con mayor densidad que el agua, o insectos, floten en la superficie, en vez de hundirse. Si solo se considera la gravedad, son olas gravitacionales; si solo se tiene en cuenta la tensión superficial, son olas capilares puras; si se tienen en cuenta ambas fuerzas, entonces son olas capilares-gravitacionales.
Además, es posible considerar estas olas con una profundidad finita o infinita; la profundidad infinita es una aproximación de la profundidad de los océanos. Para modelar olas más realistas, que tienen en cuenta también la presencia del viento, remolinos y corrientes, se añade a las ecuaciones la vorticidad, que se relaciona con la velocidad rotacional del fluido.
Por otro lado, al mirar las olas de superficie de un lago o del mar se observa que, de forma aproximada, mantienen una velocidad constante y una misma forma. Por tanto, el problema se estudia con independencia del tiempo, lo que permite simplificar las ecuaciones de Euler. Sin embargo, por otro lado, se tiene en cuenta que la interfase entre el agua y el aire se mueve con el fluido, por lo que es una incógnita del problema, que añade dificultad matemática.
El resultado es un conjunto de ecuaciones de Euler estacionarias –es decir, cuyas soluciones no cambian con el tiempo–, incompresibles –lo que significa que el fluido no se puede comprimir, mantiene siempre el mismo volumen– y rotacionales o irrotacionales, con diferentes condiciones en la interfase (gravedad, tensión superficial o ambas). Como decíamos al comienzo, el objetivo principal es probar que tienen solución –que, en el mundo físico, se corresponde a la ola– y entender cuál es su forma y sus propiedades.
En 1840 George Gabriel Stokes comenzó sus estudios sobre las olas y descubrió que, en presencia únicamente de la gravedad, la ola más alta posible forma, en la cresta –el punto más alto de la ola–, un ángulo de 120º con el plano horizontal. La teoría de Stokes ha resultado ser muy útil para describir tsunamis y para diseñar estructuras costeras.
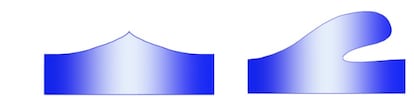
Según este resultado, considerando solo la presencia de la gravedad, no pueden aparecer olas que se doblan sobre ellas mismas (llamadas overhanging, o tubos), cuyo caso extremo son olas tan inclinadas que el extremo de la cresta toca la base, formando un tubo cerrado. Con otras condiciones, ¿podemos obtener este tipo de ola tubo como solución a las ecuaciones? Es un fenómeno que se observa en la naturaleza –de hecho, ¡son las olas favoritas de los surfistas! – por lo que, si no puede ser solución de las ecuaciones consideradas, esto significaría que el modelo no está ofreciendo una buena descripción de las olas.
De momento, hay muchas demostraciones con métodos numéricos –que aproximan las soluciones a las ecuaciones– que prueban la existencia de olas tubo en ciertas condiciones, pero pocos de estos resultados se han confirmado de forma analítica.
El resultado más famoso en ese sentido, publicado por G. D. Crapper en 1957, demuestra la existencia de olas tubo cuando solo hay tensión superficial. En concreto, prueba la existencia de olas capilares puras irrotacionales con profundidad infinita.
Desde el punto de vista analítico, estas son las únicas soluciones exactas y explícitas que muestran este comportamiento. En las últimas décadas se han realizado muchas extensiones de este trabajo, añadiendo pequeños valores de gravedad, o pequeños valores de gravedad y una vorticidad pequeña y concentrada. Todas estas soluciones se consideran perturbaciones de las olas de Crapper y tienen perfiles tubo, por lo que nos permiten acercarnos al sueño de cualquier surfista. En un planeta con una gravedad pequeña y grandes profundidades, ¡existiría una ola tubo perfecta para surfear en cualquier momento!
Elena Di Iorio es investigadora postdoctoral en el Instituto de Ciencias Matemáticas
Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.
Edición y coordinación: Ágata A. Timón G Longoria (ICMAT).
Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.




























































