Un guisante del tamaño del Sol

El parpadeo infinito de la lámpara de Thompson, de la que hablábamos la semana pasada, remite a las paradojas clásicas sobre el movimiento, como la de Aquiles y la tortuga; pero con una diferencia importante: en el mundo real, Aquiles alcanza a la tortuga, mientras que el estado final de la lámpara de Thompson es indecidible, puesto que el experimento es materialmente irrealizable (o tan siquiera concebible en el marco de la física real, puesto que no tiene sentido hablar de lapsos de tiempo infinitesimales).

Más información

El Tangram, Bolyai-Gerwien y la cuadratura del círculo

Un lector, Carlos Gaceo, ha señalado oportunamente que se echa de menos, entre tantas paradojas relacionadas con el infinito, el teorema de Banach-Tarsky, que demuestra que podemos trocear una esfera maciza y reagrupar sus fragmentos para formar dos esferas macizas iguales a la original. Una formulación más radical del teorema dice que dados dos objetos sólidos cualesquiera, uno puede ser obtenido por reagrupación de fragmentos del otro; lo que equivale a decir que a partir de una esfera del tamaño de un guisante podríamos obtener otra del tamaño del Sol. Este resultado totalmente contrario a la intuición (y al igual que la lámpara de Thompson irrealizable en el mundo físico) tiene que ver con el denominado axioma de elección, que afirma que dada una serie de conjuntos no vacíos, podemos formar otro conjunto que contenga un elemento de cada uno de ellos. La formación de dicho nuevo conjunto es trivial si partimos de un número finito de conjuntos (pues se trata simplemente de coger un elemento cualquiera de cada uno); pero, según demostró Ernst Zermelo en 1904, para un número infinito de conjuntos puede no ser así, y se hace necesaria la formulación de un axioma ad hoc. La cuestión es demasiado compleja para desarrollarla aquí, pero no quería dejar de mencionarla por su relación con lo visto en artículos anteriores; quienes deseen profundizar en el tema y aportar sus comentarios, serán bien recibidos.

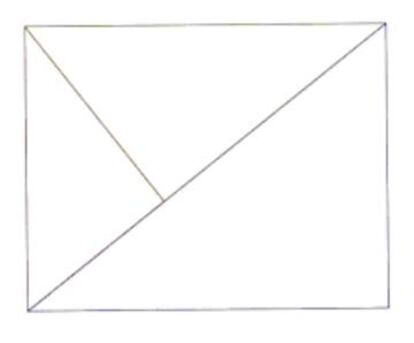
No todas las particiones y reagrupaciones son tan complejas e inquietantes como la plantada por el teorema de Branach-Tarski. En el extremo opuesto tenemos, como máxima simplificación del tangram tradicional, la elegante versión propuesta por el matemático alemán G. Brügner en 1984, que consiste en dividir un rectángulo en tres triángulos rectángulos tal como se indica en la figura. Si la relación entre los lados del rectángulo es la adecuada, podemos formar, reagrupando los tres triángulos de distintas maneras, hasta 16 figuras poligonales convexas. ¿Cuál ha de ser dicha relación tangramática?

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos Maldita física, Malditas matemáticas o El gran juego. Fue guionista de La bola de cristal.