El Tangram, Bolyai-Gerwien y la cuadratura del círculo

Quien más quien menos ha visto alguna vez un Tangram, ese juego de origen chino consistente en 7 piezas, que inicialmente están dispuestas en forma de cuadrado, con las que se pueden formar una gran variedad de figuras planas. En la siguiente imagen podéis ver la disposición inicial de las piezas del Tangram y algunos ejemplos de figuras planas creadas con dichas piezas:

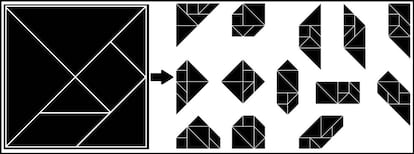
Si trasladamos esto a papel, tendríamos que podemos cortar un cuadrado en un cierto número de piezas (siete concretamente en el caso del Tangram) que pueden reordenarse para formar otras figuras (polígonos en el caso de la imagen anterior). Un ejemplo muy conocido de esto es la llamada disección de Dudeney, que transforma un cuadrado en un triángulo de la misma área. Esta disección tiene, además, la particularidad de que se pasa de una figura a otra girando las piezas cortadas mientras éstas permanecen unidas en parejas por un vértice. Podéis ver varias secuencias en la siguiente imagen:

En prof.pantaloni tenéis la disección completa animada en un gif.

A partir de esto, nos podríamos preguntar si, dado un polígono cualquiera de la misma área que un cuadrado, existiría alguna manera de cortar el cuadrado en piezas de forma que se puedan recolocar para formar dicha figura. Más general: si tenemos dos polígonos cualesquiera de la misma área, ¿podemos cortar uno en trocitos que puedan reordenarse para formar el otro? Pues la respuesta es que sí se puede, y eso nos lo asegura el llamado teorema de Bolyai-Gerwien, que se puede enunciar informalmente como sigue:

Teorema de Bolyai-Gerwien: Dados dos polígonos de la misma área, se puede cortar uno de ellos en un número finito de piezas poligonales que, mediante traslaciones y giros, pueden colocarse formando el otro polígono.

Este resultado fue conjeturado por Farkas Bolyai en 1790 y demostrado por primera vez por el matemático William Wallace (nada que ver con el protagonista de Braveheart) en 1807 (por ello, a veces este resultado se llama teorema de Wallace-Bolyai-Gerwien). En 1833, P. Gerwien (no he conseguido encontrar información fiable sobre qué significa exactamente esa P) demostró este teorema sin conocer la demostración anterior de Wallace, y en 1835 el propio Bolyai encontró una demostración también sin tener conocimiento de las pruebas anteriores de Wallace y Gerwien.

Informalmente, las líneas generales de la demostración son las siguientes:

1.- Todo polígono puede cortarse en piezas triangulares.

2.- Esas piezas triangulares pueden reordenarse formando rectángulos.

3.- Colocando conveniente esos rectángulos, se puede formar un único rectángulo.

4.- Un rectángulo puede recortarse en piezas con las que se puede formar un cuadrado.

5.- Como este proceso puede realizarse con los dos polígonos, lo que hacemos es pasar de uno de ellos a un cuadrado y después pasar de ese cuadrado al otro polígono (invirtiendo el proceso de cuadrar este polígono).

Y así conseguimos llevar un polígono a otro polígono mediante disecciones. Aquí tenéis algunos ejemplos de pasos de un polígono a otro:

Podéis ver muchos más en Geometric Dissections, de Gavin Theobald (web de donde he sacado las disecciones anteriores).

Sabiendo esto, surge de manera natural preguntarse sobre qué ocurre en tres dimensiones. Y esta cuestión es tan interesante que el propio David Hilbert la incluyó dentro de su famosa lista de 23 problemas que propuso en el Congreso Internacional de Matemáticos celebrado en París en el año 1900. El tercero de los problemas de dicha lista es el que hace alusión a este tema:

Dados dos poliedros del mismo volumen, ¿siempre se puede cortar uno de ellos en un número finito de piezas poliédricas que puedan reordenarse de manera que formen el segundo poliedro?

¿Qué creéis? Os dejo unos segundos para pensarlo…

…¿Ya? Pues la respuesta es no, no siempre se puede hacer lo que pregunta el tercer problema de Hilbert, y esta imposibilidad general fue demostrada por Max Dehn en el mismo año 1900.

Y, volviendo a las dos dimensiones, también surgió una interesante y curiosa pregunta que, en esta ocasión, se hizo Alfred Tarski. Este matemático polaco se preguntó si se podría pasar de un cuadrado a un círculo de la misma área de una forma parecida a lo que se puede hacer entre polígonos (nada que ver con la cuadratura del círculo clásica, ya que aquí no tenemos las restricciones de las construcciones griegas con regla y compás). ¿Cuál creéis que es la respuesta en este caso? De nuevo, unos segundos para que penséis y respondáis…

…

…¡¡Tiempo!! La respuesta en este caso es que sí, sí se puede, aunque la cosa tiene “truco”. Tarski conjeturó que sí se podía pasar de un cuadrado a un círculo, y el matemático húngaro Mikos Laczkovich lo demostró en 1990 en su trabajo Equidecomposability and discrepancy; a solution of Tarski’s circle-squaring problem. La demostración de Laczkovich nos dice que necesitaríamos, como mucho, 10⁵⁰ piezas (casi nada), y que las mismas son no medibles (sin entrar en detalles, raras raras) y, por tanto, ni mucho menos “cortables”.

El hecho de que no se puede pasar de un círculo a un cuadrado con piezas “cortables con tijeras” ya lo habían demostrado Lester Dubins, Morris Hirsch y Jack Karush en 1963, pero hasta hace poco seguía sin saberse si se podía hacer, al menos, con piezas medibles. El propio Laczkovich hablaba en su trabajo sobre este asunto, y lo dejaba planteado como, posiblemente, la pregunta más importante que quedaba por resolver en relación con este tema.

Bien, pues ya se ha resuelto. En el trabajo Measurable circle squaring (que será publicado próximamente en la prestigiosa revista Annals of Mathematics), Lukasz Grabowski, András Máthé y Oleg Pikhurko han demostrado que sí se puede pasar de un círculo a un cuadrado con piezas medibles. Es decir, que existe una cierta cantidad finita de piezas medibles que al colocarlas de cierta manera nos dan un cuadrado y convenientemente trasladadas nos dan un círculo.

Usando sólo traslaciones, este número de piezas (según los autores) está entre 4 y 10⁵⁰ (la cota de Laczkovich), por lo que queda todavía un gran margen para mejorar el resultado.