Fermat y los polígonos regulares

Si la semana pasada los protagonistas de El Aleph fueron los poliedros, en esta ocasión las estrellas del artículo van a ser sus “hermanos” de dos dimensiones: los polígonos. Y, más concretamente, serán los polígonos regulares los que ejercerán de actores principales de nuestra historia de hoy. Pero antes de que estos polígonos hagan acto de presencia, vamos a hablar brevemente de uno de los matemáticos más importantes de la historia de las matemáticas: Pierre de Fermat.

Pierre de Fermat fue un jurista francés del siglo XVII aficionado a las matemáticas que pasa por ser considerado el creador de la teoría de números, aunque también realizó aportes en otras áreas de las matemáticas. Fermat solía plantear resultados sin dar su demostración, y no publicó prácticamente nada en vida. Solía comunicar sus descubrimientos mediante cartas enviadas a otros matemáticos de la época (principalmente a Marin Mersenne), y debía tener “buen ojo” viendo que casi nunca se equivocó en sus afirmaciones.

Y decimos “casi” porque sí cometió algún error. El más importante es, posiblemente, considerar que había encontrado una expresión que generaba siempre números primos distintos. Fermat conjeturó que todos los números de la forma 2 elevado a 2ⁿ más 1 (el 1 se suma después de calcular las dos potencias de 2), llamados F_n, eran primos para todo número entero no negativo que pudiéramos colocar en el lugar de n.

Cierto es que para 0, 1, 2, 3 y 4 esa expresión da números primos, pero para n=5 el resultado es un número compuesto. Fue Leonhard Euler quien, un siglo más tarde, demostró este hecho factorizando F₅. En la siguiente imagen podéis ver los resultados de F_n para n de 0 a 5 y la factorización de F₅:

Es decir, no todos estos números de Fermat son primos (los que sí lo son se denominan, como no podía ser de otra forma, primos de Fermat). Pero la cosa es aún más grave: no se conoce ningún otro número de Fermat que sea primo aparte de F₀, F₁, F₂, F₃ y F₄.De alguno de los posteriores a F₅ se conoce su factorización (no son primos), y para algún otro se ha demostrado que no es primo, aunque todavía no se haya podido factorizar (dada la magnitud del número en cuestión). Vamos, que no fue un error pequeño, sino que la afirmación de Fermat en este tema fue un fallo bastante gordo.

Pero, como todo lo que tocaba Fermat, estos números escondían algo realmente interesante, una relación inesperada con una figuras planas que, en principio, no tienen mucho que ver con ellos: los polígonos regulares.

Un polígono es una figura plana formada por un número finito de segmentos, que se llaman lados, que forman una cadena cerrada y que delimitan una región del plano. Los puntos en los que se cortan dos segmentos se llaman vértices. Un cuadrado, un triángulo, un rectángulo o un pentágono son ejemplos de polígonos.

Si los lados del polígono son iguales y los ángulos que forman cada dos lados consecutivos también lo son, entonces estamos ante un polígono regular. Un cuadrado y un triángulo equilátero son polígonos regulares.

La construcción de polígonos regulares con regla y compás, siguiendo las normas griegas que ya comentamos cuando hablamos de la cuadratura del círculo, ha sido un tema tratado por muchos matemáticos desde la antigüedad. Desde hace mucho tiempo se sabe cómo construir de esta forma un triángulo equilátero, un cuadrado o un pentágono, pero, por ejemplo, no se conocía en la época de Fermat ninguna manera de construir un heptágono regular (siete lados) o un eneágono regular (nueve lados). De hecho, no se sabía si podían construirse todos, y, en el caso de que no se pudiera, no había una forma de determinar cuáles eran construibles con regla y compás y cuáles no.

Pero llegó Carl Friedrich Gauss y revolucionó el tema. En su maravillosa obra Disquisitiones Arithmeticae, Gauss demostró que si el número de lados de un polígono cumplía cierta condición, entonces era construible con regla y compás. Esa condición era que la factorización en números primos del número de lados sólo podía ser una potencia de 2, un primo de Fermat o un producto de estos tipos de números: una potencia de 2 por un primo de Fermat, un producto de varios primos de Fermat distintos o la multiplicación de una potencia de 2 por varios primos de Fermat también distintos.

Escrito de manera más “matemática”, Gauss demostró lo siguiente en la sección VII de sus Disquisitiones:

Si el número de lados, n, de un polígono regular es de la forma n=2^r · p₁ · … · p_k, con r un entero mayor o igual que cero y p₁, …, p_k primos de Fermat distintos, entonces dicho polígono regular es construible con regla y compás.

Aclaro que podría no aparecer ningún primo de Fermat en la descomposición, y recalco de nuevo que si aparece más de uno entonces deben ser distintos. Obviando ahora los casos que no tienen sentido (r=0 sin primos de Fermat daría un polígono de un lado, y r=1 sin primos de Fermat daría un polígono de dos lados), con este resultado hemos avanzado bastante en lo que se refiere a identificar los polígonos regulares construibles…

…pero todavía no está todo hecho. Si el número de lados tiene esa forma, entonces el polígono regular es construible, pero si no es de esa forma no sabemos nada todavía. Lo ideal sería que dicho resultado también fuera cierto al contrario, ¿verdad? Es decir, que también fuera cierto que si un polígono regular es construible, entonces su número de lados sigue esa expresión.

Gauss pensaba que sí, que esto también se cumplía, pero no llegó a demostrarlo (al menos no se conoce ninguna demostración suya al respecto). Lo importante es que no se equivocaba: Pierre Wantzel, en 1837, demostraba que el recíproco del resultado de Gauss también era cierto. Esto sí que cierra completamente el círculo: un polígono regular es construible con regla y compás si y sólo si su número de lados factoriza en números primos de la forma comentada antes.

Esto significa que, con las reglas clásicas griegas, podemos construir un cuadrado (2² lados), un triángulo equilátero (3 lados, primo de Fermat), un pentágono regular (5 lados, primo de Fermat), un hexágono regular (2·3 lados, producto de potencia de 2 por primo de Fermat) o un decágono regular (2·5 lados, potencia de 2 por primo de Fermat), pero no un heptágono regular ni un eneágono regular, ya que ninguno factoriza de la forma descrita.

Comentario aparte merece el heptadecágono regular, polígono regular de 17 lados (primo de Fermat). Gauss, cuando tenía ¡¡19 años!!, demostró que este polígono era construible con regla y compás, pero no dio los pasos de su construcción. Fue Jonathan Erchinger quien nos mostró cómo construir un heptadecágono regular en 64 pasos. Y también el polígono regular de 65537 lados (primo de Fermat), cuya construcción fue desarrollada, durante 10 años, por Johann Gustav Hermes. La publicó en 1894 y consta de nada menos que 200 páginas.

Viendo la factorización del número de lados de los polígonos regulares construibles, es evidente que se pueden construir infinitos de ellos con regla y compás. Pero analizando el asunto más profundamente, y teniendo en cuenta que no se conocen más primos de Fermat que F₀, F₁, F₂, F₃ y F₄, en esencia son muy pocos los polígonos regulares construibles. De hecho, si quitamos la potencia de 2 tenemos solamente 31 polígonos regulares que sabemos que son construibles. Mientras no se descubran más primos de Fermat, éstos serán los únicos de lados impares que podremos aspirar a construir. Cuando menos curioso que, teóricamente (en la práctica es prácticamente imposible), podamos construir con regla y compás un polígono regular de 4294967295 lados (3·5·17·257·65537) pero no podamos construir uno de 7 lados...

Para terminar, os animo a que expliquéis en los comentarios cómo construiríais con regla y compás (y las reglas clásicas, tenedlo en cuenta) algún polígono regular. Considerad que comenzáis con unos ejes y dos puntos, el origen, A, y otro punto, B, en el eje horizontal. Os dejo yo la más sencilla: la construcción de un triángulo equilátero:

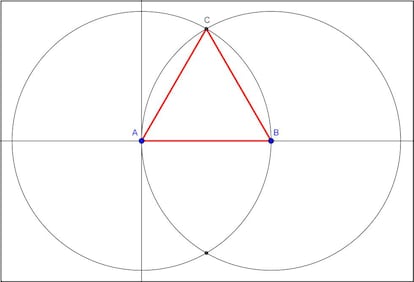
Trazamos una circunferencia con centro A y radio AB, y otra circunferencia con centro B y radio también AB. Esas dos circunferencias se cortan en dos puntos. Tomamos, por ejemplo, el superior, C, y trazamos los segmento AB, AC y BC. Esos tres segmentos forman un triángulo equilátero.

Aquí tenéis una imagen con la construcción: