Unos dados muy traviesos

Si Pedro es más alto que Juan, y Juan es más alto que Luis, está claro que Pedro también es más alto que Luis. Sin embargo, si Pedro es amigo de Juan, y Juan es amigo de Luis, Pedro no tiene por qué ser amigo de Luis. Esta propiedad de las relaciones entre ciertos elementos se denomina en matemáticas propiedad transitiva, y, como acabamos de ver, puede cumplirse o no dependiendo del tipo de elementos que comparemos y de la relación que queramos establecer entre ellos.

Básicamente, decimos que se cumple la propiedad transitiva en un conjunto y con una relación si, en todos los casos en los que un elemento A está relacionado con un elemento B, y B está relacionado con un elemento C, entonces se cumple que A está relacionado con C.

Como hemos visto antes, esta propiedad no siempre se cumple, y en nuestro entorno podemos encontrar muchos ejemplos. Y hay un juego muy popular que tampoco la cumple: el piedra, papel, tijera: papel gana a piedra, piedra gana a tijera pero papel no gana a tijera.

Este juego es así porque nosotros hemos establecido estas normas, por lo que podríamos decir que hemos definido el juego para que sea no transitivo. Ciñéndonos a matemáticas, quizás podría parecer que es más complicado encontrar una situación como ésta, en la que se invierten los papeles en la relación de transitividad. Si piensas eso sigue leyendo, y si no lo piensas también.

Vamos a plantear un juego con dados. Pero no con unos dados “habituales”, de los de siempre, sino con unos dados muy particulares. Son estos tres:

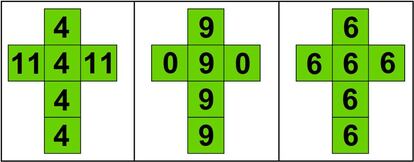
La idea es que elijáis uno de los dados para jugar contra mí, que elegiré otro después (os dejo elegir primero, mira que soy bueno…). Cuando hayamos elegido, tiramos los dos dados y anotamos la puntuación obtenida en cada uno. Si en cada tirada gana la mayor puntuación, y vosotros queréis ganarme, ¿qué dado elegiríais para jugar? Esto es, ¿qué dado os proporcionaría una mayor probabilidad de ganarme?

Si queréis pensar un poco sobre ello parad de leer y analizad la situación. Si ya lo habéis pensado (o si no os apetece mucho darle vueltas al coco) continuad leyendo.

Vamos a analizar las probabilidades de cada uno de los tres enfrentamientos para ver cuál os convendría elegir para jugar.

Comparemos primeros el primer dado de la izquierda, llamémosle dado A, con el del centro, que será el dado B. Aquí tenéis una tabla con todos los posibles resultados, en la que he coloreado de azul los casos en los que gana el dado A y en verde los casos en los que gana el dado B:

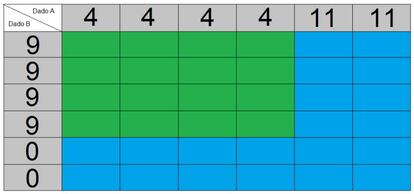
Como podéis ver, el dado A gana más veces que el B, 20 a 16. Por tanto, no os interesa elegir el dado B, porque en ese caso yo elegiría el dado A y, a la larga, os acabaría ganando (la probabilidad de que yo gane sería mayor).

Ahora comparemos el B con el de la derecha, que llamaremos dado C. En la siguiente tabla podéis ver cómo quedaría la cosa (B en verde y C en morado):

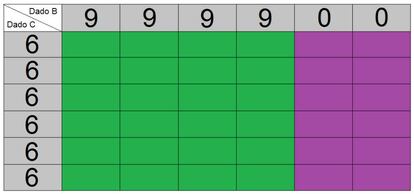
En este caso, vemos que el dado B gana más veces que el C, 24 a 12. Esto significa que tampoco os interesa elegir el C, ya que yo elegiría el B y tendría mayor probabilidad de ganaros.

Bien, la cosa parece clara: si no os interesa elegir el B (porque pierde con el A) ni el C (porque pierde con el B), entonces conviene que elijáis el A, ¿verdad? Sí, sí, elegid el A…y yo elegiré el C:

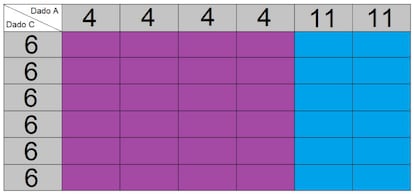
Como se puede ver en la tabla, el dado C gana más veces que el A, de nuevo 24 a 12.

Tenemos entonces que el dado A gana al dado B, el dado B gana al dado C y el dado C gana al dado A, un “piedra, papel, tijera” pero con dados. Esto significa que elijáis el dado que elijáis, lo más probable es que siempre gane yo, ya que siempre podré elegir un dado con mayor probabilidad de ganar que el vuestro (quizás en realidad no sea tan bueno dejándoos elegir primero…).

Estos dados tan traviesos se denominan dados no transitivos, porque, como acabamos de ver, no cumplen la propiedad transitiva (si A gana a B y B gana a C, entonces A debería ganar a C, pero hemos visto que no es así). Este ejemplo no es ni mucho menos el único, existen mucho juegos de tres dados no transitivos…y también con cuatro dados, y con cinco, y general se pueden construir ciclos con el número de dados queramos donde el primero gana al segundo, el segundo al tercero, y así sucesivamente hasta el último, que gana al primero.

Una última curiosidad sobre estos dados. Imaginaos que ahora cada uno tiene que tirar su dado dos veces y sumar la puntuación. ¿Qué dado elegiríais ahora? Pensad, que también os dejo elegir primero…

…¿Lo habéis pensado? Bueno, sea como sea os cuento. En este caso también estáis perdidos, si elegís primero la probabilidad de que yo gane sigue siendo mayor que la vuestra. Lo curioso es que las ventajas entre los dados se invierten. Es decir, en este nuevo juego el dado B gana al dado A, el dado C gana al dado B y el dado A gana al dado C. Os invito a que creéis vosotros unas tablas parecidas a las que os he mostrado en este artículo para esta modalidad del juego y que veáis así claramente esta inversión de ventajas.

Posiblemente, haya lectores que piensen que esto de los dados no transitivos es una mera curiosidad probabilística sin mayor interés, pero creo que en realidad no es así. El mero hecho de que los juegos de dados no transitivos puedan construirse con el número que queramos de ellos ya tiene cierto interés. Pero la cosa no se queda ahí. En las altas esferas matemáticas también tiene interés este tema de los dados no transitivos. De hecho, Tim Gowers (medalla Fields en 1998) ha comenzado un proyecto tipo polymath en su blog sobre dados intransitivos. Los proyectos polymath son algo así como problemas interesantes sin resolver que se proponen para que matemáticos de todo el mundo los estudien en conjunto. En PolyMath Wiki podéis ver los que se han propuesto en la web oficial y algunos de los que se están estudiando mediante propuestas en otras webs. Éste de los dados no transitivos se propuso a raíz del trabajo Intransitive Dice (de Brian Conrey, James Gabbard, Katie Grant, Andrew Liu y Kent Morrison) y trata de descubrir cómo de rara es esta no-transitividad.

Y para finalizar, una anécdota relacionada con estos dados. Se cuenta que en una ocasión el magnate estadounidense Warren Buffett, muy aficionado a los juegos de azar, ofreció a Bill Gates jugar con un conjunto de dados no transitivos, dejando que Gates escogiera primero. Al parecer, Gates tomó los dados y los analizó durante unos instantes…y aceptó el juego, pero cediéndole a Buffett el primer turno de elección. No es tonto el señor Gates, no…